题目内容
已知函数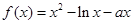 ,
, .
.
(1)当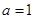 时,求
时,求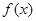 的最小值;
的最小值;
(2)若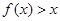 ,求a的取值范围.
,求a的取值范围.
(1)0;(2)(-∞,0).
解析试题分析:本题主要考查导数的计算、利用导数判断函数的单调性、利用导数求函数的最值、恒成立问题等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,对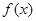 求导,利用“
求导,利用“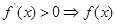 单调递增,
单调递增,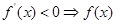 单调递减”判断函数的单调性,确定函数最值的位置,并求出函数的最小值;第二问,先将已知不等式进行转化,将所求的参数分离出来,构造新的函数,利用“
单调递减”判断函数的单调性,确定函数最值的位置,并求出函数的最小值;第二问,先将已知不等式进行转化,将所求的参数分离出来,构造新的函数,利用“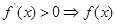 单调递增,
单调递增,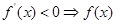 单调递减”判断函数的单调性,确定函数最值的位置,并求出函数的最值,代入到所转化的式子中即可.
单调递减”判断函数的单调性,确定函数最值的位置,并求出函数的最值,代入到所转化的式子中即可.
试题解析:(1)当a=1时,f(x)=x2-lnx-x,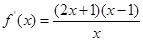 .
.
当x∈(0,1)时,f¢(x)<0;当x∈(1,+∞)时,f¢(x)>0.
所以f(x)的最小值为f(1)=0. 5分
(2)f(x)>x,即f(x)-x=x2-lnx-(a+1)x>0.
由于x>0,所以f(x)>x等价于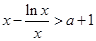 . 7分
. 7分
令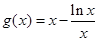 ,则
,则 .
.
当x∈(0,1)时,g¢(x)<0;当x∈(1,+∞)时,g¢(x)>0.
g(x)有最小值g(1)=1.
故a+1<1,a的取值范围是(-∞,0). 12分
考点:导数的计算、利用导数判断函数的单调性、利用导数求函数的最值、恒成立问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
.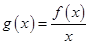 ,当
,当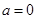 时,讨论
时,讨论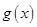 的单调性;
的单调性;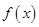 在
在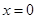 处取得极小值,求
处取得极小值,求 的取值范围.
的取值范围.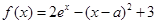 ,
,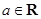 .
.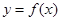 的图象在
的图象在 处的切线与
处的切线与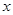 轴平行,求
轴平行,求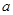 的值;
的值;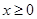 ,
,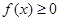 恒成立,求
恒成立,求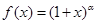 的定义域是
的定义域是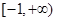 ,其中常数
,其中常数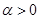 .
.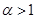 ,求
,求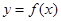 的过原点的切线方程.
的过原点的切线方程.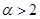 时,求最大实数
时,求最大实数 ,使不等式
,使不等式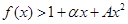 对
对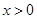 恒成立.
恒成立.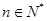 ,有
,有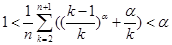 .
.
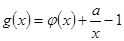 在点
在点 处的切线与直线
处的切线与直线 平行,求
平行,求 的值;
的值; ,
,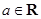 ,且
,且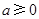 .求函数
.求函数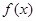 的单调递增区间.
的单调递增区间.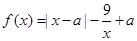 ,
,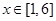 ,
,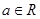 .
.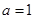 ,试判断并用定义证明函数
,试判断并用定义证明函数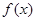 的单调性;
的单调性;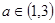 时,求函数
时,求函数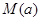 .
.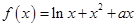 ,
,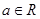 .
. 在其定义域上为增函数,求
在其定义域上为增函数,求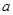 的取值范围;
的取值范围;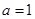 时,函数
时,函数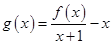 在区间
在区间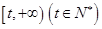 上存在极值,求
上存在极值,求 的最大值.
的最大值. ≈
≈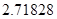 ).
).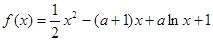
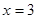 是
是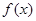 的极值点,求
的极值点,求 的范围,使得
的范围,使得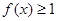 恒成立.
恒成立.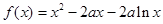 ,
,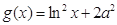 ,其中
,其中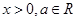 .
.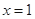 是函数
是函数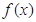 的极值点,求
的极值点,求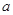 的值;
的值;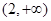 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;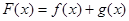 ,求证:
,求证: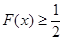 .
.