题目内容
知函数y=sin2x+sin2x+3cos2x,求(1)函数的最小值及此时的x的集合;
(2)函数的单调减区间;
(3)此函数的图象可以由函数
 的图象经过怎样变换而得到.
的图象经过怎样变换而得到.
【答案】分析:(1)利用两角和公式和二倍角公式对函数解析式化简整理,利用正弦函数的性质求得函数的最小值以及x的值.
(2)利用正弦函数的单调性,求得函数的单调减区间.
(3)先由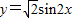 的图象向左平移
的图象向左平移 个单位,再向上平移2个单位而得到.y=
个单位,再向上平移2个单位而得到.y=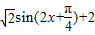 的图象.
的图象.
解答:解:由y=sin2x+sin2x+3cos2x=1+sin2x+2cos2x=1+sin2x+(1+cos2x)=
(1)当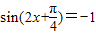 时,y最小=2-
时,y最小=2-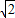 ,此时,由2x+
,此时,由2x+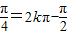 ,得x=kπ-
,得x=kπ-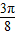 ,
,
(2)由2kπ+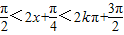 ,得减区间为
,得减区间为
(3)其图象可由y=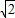 sin2x的图象向左平移
sin2x的图象向左平移 个单位,再向上平移2个单位而得到.
个单位,再向上平移2个单位而得到.
点评:本题主要考查了三角函数的最值,两角和公式和二倍角公式的化简求值.考查了考生基础知识和基本能力.
(2)利用正弦函数的单调性,求得函数的单调减区间.
(3)先由
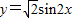 的图象向左平移
的图象向左平移 个单位,再向上平移2个单位而得到.y=
个单位,再向上平移2个单位而得到.y=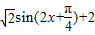 的图象.
的图象.解答:解:由y=sin2x+sin2x+3cos2x=1+sin2x+2cos2x=1+sin2x+(1+cos2x)=

(1)当
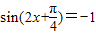 时,y最小=2-
时,y最小=2-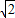 ,此时,由2x+
,此时,由2x+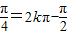 ,得x=kπ-
,得x=kπ-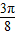 ,
,(2)由2kπ+
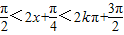 ,得减区间为
,得减区间为
(3)其图象可由y=
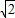 sin2x的图象向左平移
sin2x的图象向左平移 个单位,再向上平移2个单位而得到.
个单位,再向上平移2个单位而得到.点评:本题主要考查了三角函数的最值,两角和公式和二倍角公式的化简求值.考查了考生基础知识和基本能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数y=sin2x,则( )
| A、有最小正周期为2π | ||
| B、有最小正周期为π | ||
C、有最小正周期为
| ||
| D、无最小正周期 |