题目内容
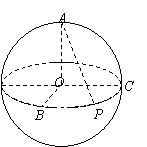
 如图,A、B、C是球面上三点,且AB=2cm,BC=4cm,∠ABC=60°,若球心O到截面ABC的距离为2
如图,A、B、C是球面上三点,且AB=2cm,BC=4cm,∠ABC=60°,若球心O到截面ABC的距离为2| 2 |
分析:由题意可知三角形ABC 是直角三角形,BC为小圆的直径,球心O到截面ABC的距离为2
cm,就是O到BC的中点的距离,求出球的半径,即可求出球的表面积.
| 2 |
解答:解:A、B、C是球面上三点,且AB=2cm,BC=4cm,∠ABC=60°,所以三角形ABC 是直角三角形,BC为小圆的直径,
球心O到截面ABC的距离为2
cm,就是O到BC的中点的距离,所以球的半径为:
=2
所以球的表面积为:4π(2
)2=48π cm2.
故答案为:48π
球心O到截面ABC的距离为2
| 2 |
(2
|
| 3 |
所以球的表面积为:4π(2
| 3 |
故答案为:48π
点评:本题是基础题,考查球的表面积,球的内接体的知识,判断三角形的形状以及准确找出球的半径与ABC 的小圆的关系,是本题的关键,考查空间想象能力,计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
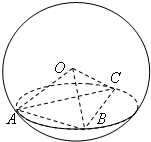
 如图,A、B、C是球O的球面上三点,且OA、OB、OC两两垂直,P是球O的大圆上BC弧上的中点,则直线AP与OB所成角的弧度数是
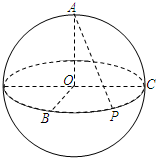
如图,A、B、C是球O的球面上三点,且OA、OB、OC两两垂直,P是球O的大圆上BC弧上的中点,则直线AP与OB所成角的弧度数是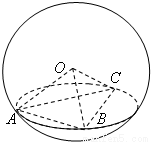 如图,A、B、C是球面上三点,且AB=2cm,BC=4cm,∠ABC=60°,若球心O到截面ABC的距离为2
如图,A、B、C是球面上三点,且AB=2cm,BC=4cm,∠ABC=60°,若球心O到截面ABC的距离为2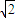 cm,则该球的表面积为 cm2.
cm,则该球的表面积为 cm2.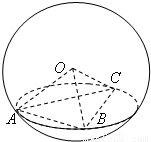 如图,A、B、C是球面上三点,且AB=2cm,BC=4cm,∠ABC=60°,若球心O到截面ABC的距离为2
如图,A、B、C是球面上三点,且AB=2cm,BC=4cm,∠ABC=60°,若球心O到截面ABC的距离为2 cm,则该球的表面积为 cm2.
cm,则该球的表面积为 cm2.