题目内容
已知
<a<1,若f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),记g(a)=M(a)-N(a).
(1)求g(a)的解析表达式;
(2)若对一切a∈(
,1)都有kg(a)-1<0成立,求实数k的取值范围.
| 1 |
| 3 |
(1)求g(a)的解析表达式;
(2)若对一切a∈(
| 1 |
| 3 |
分析:(1)将f(x)=ax2-2x+1配方化为f(x)=a(x-
)2+1-
,由
<a<1可求1<
<3,求得N(a);根据f(x)的对称轴x=
在区间[1,3]的位置情况分类讨论,求得M(a),从而求得g(a)的解析表达式;
(2)对g(a)=
,分段研究函数的单调性,从而可求得各段上g(a)及
的取值范围,及k满足的关系式,再利用“小小取小”的恒成立思想即可解决问题.
| 1 |
| a |
| 1 |
| a |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| a |
(2)对g(a)=
|
| 1 |
| g(a) |
解答:解:(1)f(x)=a(x-
)2+1-
x∈[1,3]
由
<a<1知,1<
<3.从而N(a)=1-
∴当1<
≤2即
≤a<1时,M(a)=f(3)=9a-5
当2<
<3即
<a<
时,M(a)=f(1)=a-1
∴g(a)=
(2)当
<a<
时,g(a)=a+
-2为减函数.
∴
<g(a)<
.
要使kg(a)-1<0恒成立,则k<
恒成立.而
<
<2
∴k≤
.
又当
≤a<1时,g(a)=9a+
-6=9(a+
)-6为增函数
∴
≤g(a)<4
要使kg(a)-1<0恒成立.则k<
恒成立.而
<
≤2
∴k≤
综上得,k≤
.
| 1 |
| a |
| 1 |
| a |
由
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| a |
∴当1<
| 1 |
| a |
| 1 |
| 2 |
当2<
| 1 |
| a |
| 1 |
| 3 |
| 1 |
| 2 |
∴g(a)=
|
(2)当
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| a |
∴
| 1 |
| 2 |
| 4 |
| 3 |
要使kg(a)-1<0恒成立,则k<
| 1 |
| g(a) |
| 3 |
| 4 |
| 1 |
| g(a) |
∴k≤
| 3 |
| 4 |
又当
| 1 |
| 2 |
| 1 |
| a |
| ||
| a |
∴
| 1 |
| 2 |
要使kg(a)-1<0恒成立.则k<
| 1 |
| g(a) |
| 1 |
| 4 |
| 1 |
| g(a) |
∴k≤
| 1 |
| 4 |
综上得,k≤
| 1 |
| 4 |
点评:本题考查二次函数在闭区间上的最值,着重考查学生分类讨论思想与转化思想及恒成立思想的应用,中档题.

练习册系列答案
相关题目
 n=
n= .
. 的值;
的值; 中,角A,B,C的对边分别是a,b,c,且满足
中,角A,B,C的对边分别是a,b,c,且满足 求f(A)的取值范围.
求f(A)的取值范围.  n=
n= .
. 的值;
的值; 中,角A,B,C的对边分别是a,b,c,且满足
中,角A,B,C的对边分别是a,b,c,且满足 求f(A)的取值范围.
求f(A)的取值范围.

 取得最小值时点P的坐标.
取得最小值时点P的坐标.  是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆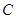 于
于 两点
两点 ,求直线
,求直线 的方程;
的方程; 恒过一定点.
恒过一定点.