题目内容
设集合A是实数集R的子集,如果点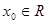 满足:对任意
满足:对任意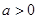 ,都存在
,都存在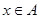 使得
使得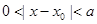 ,则称
,则称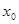 为集合A的聚点.用Z表示整数集,则在下列集合中,以0为聚点的集合有( )
为集合A的聚点.用Z表示整数集,则在下列集合中,以0为聚点的集合有( )
(1)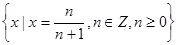 (2)不含0的实数集R
(2)不含0的实数集R
(3)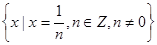 (4)整数集Z
(4)整数集Z
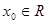 满足:对任意
满足:对任意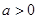 ,都存在
,都存在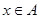 使得
使得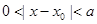 ,则称
,则称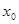 为集合A的聚点.用Z表示整数集,则在下列集合中,以0为聚点的集合有( )
为集合A的聚点.用Z表示整数集,则在下列集合中,以0为聚点的集合有( )(1)
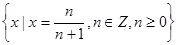 (2)不含0的实数集R
(2)不含0的实数集R(3)
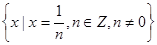 (4)整数集Z
(4)整数集Z| A.(1)(3) | B.(1)(4) | C.(2)(3) | D.(1)(2)(4) |
C.
试题分析:(1)中,集合
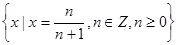 中的元素是极限为1的数列,除了第一项0之外,其余的都至少比0大
中的元素是极限为1的数列,除了第一项0之外,其余的都至少比0大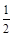 ,∴在
,∴在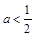 的时候,不存在满足
的时候,不存在满足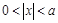 的
的 ,∴0不是集合
,∴0不是集合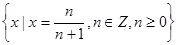 的聚点;(2)集合
的聚点;(2)集合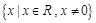 ,对任意的
,对任意的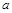 ,都存在
,都存在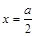 (实际上任意比
(实际上任意比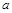 小的数都可以),使得
小的数都可以),使得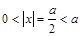 ,∴0是集合
,∴0是集合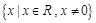 的聚点;(3)集合
的聚点;(3)集合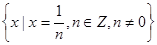 中的元素是极限为0的数列,对于任意的
中的元素是极限为0的数列,对于任意的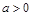 ,存在
,存在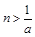 ,使
,使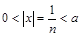 ,∴0是集合
,∴0是集合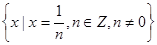 的聚点;(4)对于某个
的聚点;(4)对于某个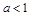 ,比如
,比如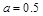 ,此时对任意的
,此时对任意的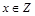 ,都有
,都有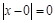 或者
或者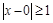 ,也就是说不可能
,也就是说不可能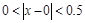 ,从而0不是整数集Z的聚点.由以上讨论知选C.
,从而0不是整数集Z的聚点.由以上讨论知选C. 
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
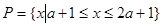 ,集合
,集合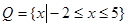
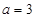 ,求集合
,求集合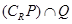 ; (2)若
; (2)若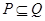 ,求实数
,求实数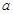 的取值范围
的取值范围 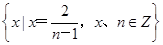 ,则∁UA=________.
,则∁UA=________. 中,被
中,被 除所得余数为
除所得余数为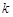 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为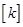 ,即
,即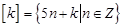 ,
,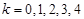 .给出如下四个结论:
.给出如下四个结论: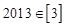 ;
;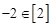 ;
; ;
;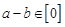 ”整数
”整数 属于同一“类”.
属于同一“类”.
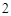
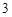
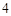
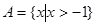 ,那么..( )
,那么..( )


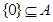
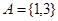 ,用描述法可以表示为 .
,用描述法可以表示为 .  满足:当
满足:当 时,有
时,有 ,给出如下三个命题:
,给出如下三个命题: 则
则 ;②若
;②若 则
则 ; ③若
; ③若 则
则 .
.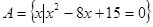 ,
,
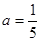 ,试判定集合A与B的关系;
,试判定集合A与B的关系;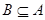 ,求实数a的取值集合.
,求实数a的取值集合.