题目内容
如图,在△ABC中,∠ABC=60°,∠BAC=90°,AD是高,沿AD把△ABD折起,使∠BDC=90°.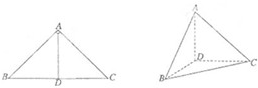
(Ⅰ)证明:平面ADB⊥平面BDC;
(Ⅱ)设E为BC的中点,求
| AE |
| DB |
分析:(Ⅰ)翻折后,直线AD与直线DC、DB都垂直,可得直线与平面BDC垂直,再结合AD是平面ADB内的直线,可得平面ADB与平面垂直;
(Ⅱ)以D为原点,建立空间直角坐标系,分别求出D、B、C、A、E的坐标,从而得出向量
、
的坐标,最后根据空间向量夹角余弦公式,计算出
与
夹角的余弦值.
(Ⅱ)以D为原点,建立空间直角坐标系,分别求出D、B、C、A、E的坐标,从而得出向量
| AE |
| DB |
| AE |
| DB |
解答: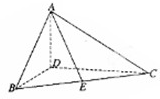 解:(Ⅰ)∵折起前AD是BC边上的高,
解:(Ⅰ)∵折起前AD是BC边上的高,
∴当△ABD折起后,AD⊥DC,AD⊥DB,
又DB∩DC=D,
∴AD⊥平面BDC,
∵AD?平面ADB
∴平面ADB⊥平面BDC
(Ⅱ)由∠BDC=90°及(Ⅰ)知DA,DB,DC两两垂直,
不防设|DB|=1,以D为坐标原点,
分别以
、
、
所在直线x,y,z轴建立如图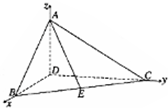 所示的空间直角坐标系,
所示的空间直角坐标系,
易得D(0,0,0),B(1,0,0),C(0,3,0),
A(0,0,
),E(
,
,0),
∴
=(
,
,-
),
=(1,0,0),
∴
与
夹角的余弦值为
cos<
,
>=
=
=
.
 解:(Ⅰ)∵折起前AD是BC边上的高,
解:(Ⅰ)∵折起前AD是BC边上的高,∴当△ABD折起后,AD⊥DC,AD⊥DB,
又DB∩DC=D,
∴AD⊥平面BDC,
∵AD?平面ADB
∴平面ADB⊥平面BDC
(Ⅱ)由∠BDC=90°及(Ⅰ)知DA,DB,DC两两垂直,
不防设|DB|=1,以D为坐标原点,
分别以
| DB |
| DC |
| DA |
 所示的空间直角坐标系,
所示的空间直角坐标系,易得D(0,0,0),B(1,0,0),C(0,3,0),
A(0,0,
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
∴
| AE |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| DB |
∴
| AE |
| DB |
cos<
| AE |
| DB |
| ||||
|
|
| ||||
1×
|
| ||
| 22 |
点评:图中DA、DB、DC三条线两两垂直,以D为坐标原点建立坐标系,将空间的几何关系的求解化为代数计算问题,使立体几何的计算变得简单.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知