题目内容
已知椭圆的两个焦点F1(-| 3 |
| 3 |
(I)求椭圆的方程;
(Ⅱ)若过点(1,0)的直线l与椭圆交于不同两点P、Q,试问在x轴上是否存在定点E(m,0),使
| PE |
| QE |
分析:(I)由题意知c=
,4a=8,b=1,由此能求出椭圆的方程.
(II)当直线l的斜率存在时,设其斜率为k,则l的方程为y=k(x-1),
,消去y得(4k2+1)x2-8k2x+4k2-4=0,P(x1,y1),Q(x2,y2),然后由韦达定理结合题设条件进行求解.
| 3 |
(II)当直线l的斜率存在时,设其斜率为k,则l的方程为y=k(x-1),
|
解答:解:(I)由题意知c=
,4a=8,∴a=2,b=1
∴椭圆的方程为
+y2=1
(II)当直线l的斜率存在时,设其斜率为k,则l的方程为y=k(x-1)
消去y得(4k2+1)x2-8k2x+4k2-4=0
设P(x1,y1),Q(x2,y2)
则由韦达定理得 x1+x2=
,x1x2=
则
=(m-x1,-y1),
=(m-x2,-y2)
=(m-x1)(m-x2)+y1y2=m2-m(x1+x2)+x1x2+y1y2
=m2-m(x1+x2)+x1x2+k2(x1-1)(x2-1)
=m2-m
+
+k2(
-
+1)
=
要使上式为定值须
=
,解得m=
∴
为定值
当直线l的斜率不存在时P(1,
),Q(1,-
) 由 E(
,0)可得
=(
,-
),
=(
,
)
∴
•
=
-
=
综上所述当E(
,0) 时,
为定值
.
| 3 |
∴椭圆的方程为
| x2 |
| 4 |
(II)当直线l的斜率存在时,设其斜率为k,则l的方程为y=k(x-1)
|
设P(x1,y1),Q(x2,y2)
则由韦达定理得 x1+x2=
| 8k2 |
| 4k2+1 |
| 4k2-4 |
| 4k2+1 |
则
| PE |
| QE |
| PE? |
| QE |
=m2-m(x1+x2)+x1x2+k2(x1-1)(x2-1)
=m2-m
| 8k2 |
| 4k2+1 |
| 4k2-4 |
| 4k2+1 |
| 4k2-4 |
| 4k2+1 |
| 8k2 |
| 4k2+1 |
=
| (4m2-8m+1)k2+(m2-4) |
| 4k2+1 |
要使上式为定值须
| m2-8m+1 |
| m2-4 |
| 4 |
| 1 |
| 17 |
| 8 |
| PE? |
| QE |
| 33 |
| 64 |
当直线l的斜率不存在时P(1,
| ||
| 2 |
| ||
| 2 |
| 17 |
| 8 |
| PE |
| 9 |
| 8 |
| ||
| 2 |
| QE |
| 9 |
| 8 |
| ||
| 2 |
∴
| PE |
| QE |
| 81 |
| 64 |
| 3 |
| 4 |
| 33 |
| 64 |
综上所述当E(
| 17 |
| 8 |
| PE? |
| QE |
| 33 |
| 64 |
点评:本题考查直线和圆锥曲线的综合运用,解题时要认真审题,有效地挖掘题设中的隐含条件,注意合理地进行等价转化.

练习册系列答案
相关题目
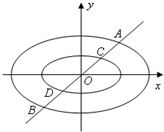 定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆 的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B.
的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B. ,求直线l的方程;
,求直线l的方程; ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围.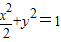 的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B.
的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B. ,求直线l的方程;
,求直线l的方程; ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围. .
. ,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由;
,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由; 和
和 分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
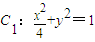 .
. ,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由;
,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由; 和
和 分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)