题目内容
(文)本题共有3个小题,第1、2小题满分各5分,第3小题满分7分.第3小题根据不同思维层次表现予以不同评分.
对于数列{an}
(1)当{an}满足an+1-an=d(常数)且
=q(常数),证明:{an}为非零常数列.
(2)当{an}满足an+12-an2=d'(常数)且
=q′(常数),判断{an}是否为非零常数列,并说明理由.
(3)对(1)、(2)等式中的指数进行推广,写出推广后的一个正确结论(不用说明理由).
对于数列{an}
(1)当{an}满足an+1-an=d(常数)且
| an+1 |
| an |
(2)当{an}满足an+12-an2=d'(常数)且
| ||
|
(3)对(1)、(2)等式中的指数进行推广,写出推广后的一个正确结论(不用说明理由).
(1)(法一)
?qan-an=d?(q-1)an=d
当q=1时,∵an≠0,所以d=0;
当q≠1时,?an=
是一常数,矛盾,所以{an}为非零常数列; (5分)
(法二)设an=a1+(n-1)d,则有:
=
=q,
即a1+nd=(a1q-qd)+qdn(2分)
所以
,解得
.由此可知数列{an}为非零常数列; (5分)
(2)记an2=bn,由(1)证明的结论知:{an2}为非零常数列.(2分)
显然,{an2}为非零常数列时,{an}不一定为非零常数列,如:非常数数列an=(-p)n(p为大于0的正常数)和常数列an=p(p为非零常数)均满足题意要求.(5分)
(3)若{an}满足an+1m-anm=d'(常数)且
=q′(常数),则当m为奇数时,{an}必为非零常数列;当m为偶数时,{an}不一定为非零常数列.
或者:设anm=a1m+(n-1)d,即anm=A+Bn,则
=(
)m=q′,即(1+
)m对一切n∈N*均为常数,则必有B=0,即有anm=A,当m为奇数时,an=
,当m为偶数时,an=
(A>0)或者an=
i (A<0).3°{an}满足an+1m-anm=d'(常数)且
=q′(常数),且m、l为整数,
当m、l均为奇数时,{an}必为非零常数列;否则{an}不一定为常数列.
事实上,条件
=q′(正常数)可以转化为
=(q′)
(常数),整个问题转化为2°,结论显然成立.(结论5分)
或者:设anm=a1m+(n-1)d,即anm=A+Bn,当m为奇数时,有an=
,则
=(
)
=q′,即(1+
)
对一切n∈N*均为常数,则必有B=0,即有anm=A,则an=
,当m为偶数时,如反例:an=(-1)nn∈N*,它既满足m次方后是等差数列,又是l(不管l为奇数还是偶数)次方后成等比数列,但它不为常数列.4°{an}满足an+1m-anm=d'(常数)且
=q′(常数),m、l为有理数,q′>0,则{an}必为非零常数列;否则{an}不一定为常数列.
证明过程同3°(结论6分)5°{an}满足an+1m-anm=d'(常数)且
=q′(常数),且m、l为实数,q′>0,{an}是不等于1的正数数列,则{an}必为非零且不等于1的常数列;否则{an}不一定为常数列.
事实上,当q′>0,m、l为实数时,条件
=q′同样可以转化为
=(q′)
,记anm=bn,由第(1)题的结论知:{bn}必为不等于1的正常数数列,也即{anm}为不等于1的正常数数列,an=
,从而{an}也是不等于1的正常数数列.
(结论7分)
|
当q=1时,∵an≠0,所以d=0;
当q≠1时,?an=
| d |
| q-1 |
(法二)设an=a1+(n-1)d,则有:
| an+1 |
| an |
| a1+(n+1-1)d |
| a1+(n-1)d |
即a1+nd=(a1q-qd)+qdn(2分)
所以
|
|
(2)记an2=bn,由(1)证明的结论知:{an2}为非零常数列.(2分)
显然,{an2}为非零常数列时,{an}不一定为非零常数列,如:非常数数列an=(-p)n(p为大于0的正常数)和常数列an=p(p为非零常数)均满足题意要求.(5分)
(3)若{an}满足an+1m-anm=d'(常数)且
| ||
|
或者:设anm=a1m+(n-1)d,即anm=A+Bn,则
| ||
|
| A+(n+1)B |
| A+nB |
| B |
| A+Bn |
| m | A |
| m | A |
| m | (-A) |
| ||
|
当m、l均为奇数时,{an}必为非零常数列;否则{an}不一定为常数列.
事实上,条件
| ||
|
| ||
|
| m |
| l |
或者:设anm=a1m+(n-1)d,即anm=A+Bn,当m为奇数时,有an=
| m | A+Bn |
| ||
|
| A+(n+1)B |
| A+nB |
| l |
| m |
| B |
| A+Bn |
| l |
| m |
| m | A |
| ||
|
证明过程同3°(结论6分)5°{an}满足an+1m-anm=d'(常数)且
| ||
|
事实上,当q′>0,m、l为实数时,条件
| ||
|
| ||
|
| m |
| l |
| m | bn |
(结论7分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
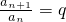 (常数),证明:{an}为非零常数列.
(常数),证明:{an}为非零常数列.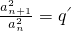 (常数),判断{an}是否为非零常数列,并说明理由.
(常数),判断{an}是否为非零常数列,并说明理由.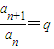 (常数),证明:{an}为非零常数列.
(常数),证明:{an}为非零常数列.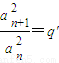 (常数),判断{an}是否为非零常数列,并说明理由.
(常数),判断{an}是否为非零常数列,并说明理由.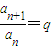 (常数),证明:{an}为非零常数列.
(常数),证明:{an}为非零常数列.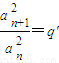 (常数),判断{an}是否为非零常数列,并说明理由.
(常数),判断{an}是否为非零常数列,并说明理由.