题目内容
在等差数列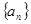 中
中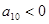 ,
,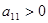 ,且
,且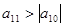 ,则在
,则在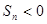 中,
中,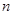 的最大值为( )
的最大值为( )
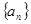 中
中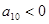 ,
,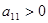 ,且
,且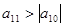 ,则在
,则在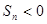 中,
中,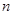 的最大值为( )
的最大值为( )| A.17 | B.18 | C.19 | D.20 |
C
试题分析:根据题意可知等差数列
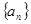 中
中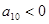 ,
,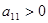 ,且
,且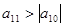 ,可知公差小于零,第11项比第10项的绝对值大,那么可知
,可知公差小于零,第11项比第10项的绝对值大,那么可知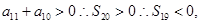 可知
可知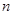 的最大值为19,故选C.
的最大值为19,故选C.点评:本题是一个最大值的问题,主要是利用等差数列的性质与等差数列的前n项和的公式以及结合二次函数的性质来解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 满足:
满足: ,则
,则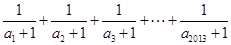 的值所在区间是( )
的值所在区间是( )


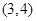
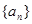 是等差数列,且
是等差数列,且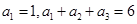
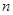 项的和
项的和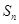
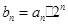 ,求
,求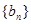 的前
的前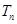
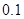 米,
米, 米,
米, 米,…,
米,…, 米或
米或 米;
米; 米时,机器人每相邻两个迈步动作恰需间隔
米时,机器人每相邻两个迈步动作恰需间隔 米(允许超出
米(允许超出 秒
秒 秒
秒  秒
秒 秒
秒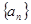 的公差大于0,且
的公差大于0,且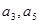 是方程
是方程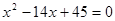 的两根,数列
的两根,数列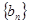 的前n项的和为
的前n项的和为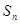 ,且
,且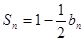 (
(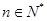 ).
).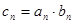 ,求证:
,求证: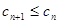 .
. 的前
的前 项和为
项和为 ,
, 、
、 是方程
是方程 的两根,且
的两根,且 ,则数列
,则数列 .
. 中,
中, , 则n=( )
, 则n=( ) }中,
}中, ,则
,则 ( )
( )