题目内容
已知A、B分别是直线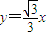 和
和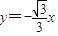 上的两个动点,线段AB的长为
上的两个动点,线段AB的长为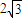 ,P是AB的中点.
,P是AB的中点.(1)求动点P的轨迹C的方程;
(2)过点Q(1,0)任意作直线l(与x轴不垂直),设l与(1)中轨迹C交于M、N,与y轴交于R点.若
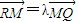 ,
,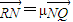 ,证明:λ+μ 为定值.
,证明:λ+μ 为定值.
【答案】分析:(1)设P(x,y),A(x1,y1),B(x2,y2),利用P是线段AB的中点,可得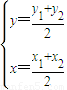 ,进而可得
,进而可得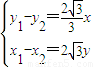 ,利用
,利用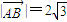 ,即可求得动点P的轨迹C的方程;
,即可求得动点P的轨迹C的方程;
(2)设直线l的方程代入椭圆方程,消去y并整理,利用韦达定理及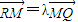 ,
,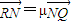 ,可得
,可得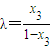 ,
,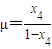 ,化简可得结论.
,化简可得结论.
解答:解:(1)设P(x,y),A(x1,y1),B(x2,y2).
∵P是线段AB的中点,∴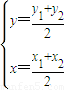 …(2分)
…(2分)
∵A、B分别是直线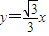 和
和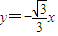 上的点,
上的点,
∴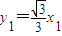 和
和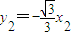 .
.
∴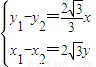 …(4分)
…(4分)
又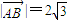 ,∴
,∴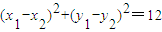 . …(5分)
. …(5分)
∴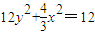 ,∴动点P的轨迹C的方程为
,∴动点P的轨迹C的方程为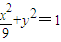 . …(8分)
. …(8分)
(2)依题意,直线l的斜率存在,故可设直线l的方程为y=k(x-1).
设M(x3,y3)、N(x4,y4)、R(0,y5),则M、N两点坐标满足方程组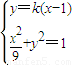
消去y并整理,得(1+9k2)x2-18k2x+9k2-9=0,…(10分)
∴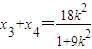 ,①
,①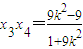 . ②…(12分)
. ②…(12分)
∵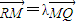 ,∴(x3,y3)-(0,y5)=λ[(1,0)-(x3,y3)].
,∴(x3,y3)-(0,y5)=λ[(1,0)-(x3,y3)].
即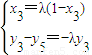 ,∴x3=λ(1-x3).
,∴x3=λ(1-x3).
∵l 与x 轴不垂直,∴x3≠1,
∴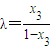 ,同理
,同理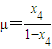 . …(14分)
. …(14分)
∴λ+μ=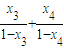 =
=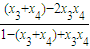 =
=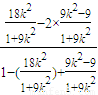 =-
=- .
.
∴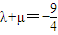 为定值. …(16分)
为定值. …(16分)
点评:本题考查动点的轨迹方程,考查直线与椭圆的位置关系,考查向量知识的运用,确定λ、μ的值是关键.
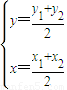 ,进而可得
,进而可得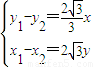 ,利用
,利用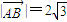 ,即可求得动点P的轨迹C的方程;
,即可求得动点P的轨迹C的方程;(2)设直线l的方程代入椭圆方程,消去y并整理,利用韦达定理及
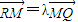 ,
,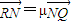 ,可得
,可得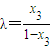 ,
,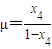 ,化简可得结论.
,化简可得结论.解答:解:(1)设P(x,y),A(x1,y1),B(x2,y2).
∵P是线段AB的中点,∴
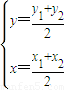 …(2分)
…(2分)∵A、B分别是直线
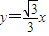 和
和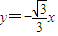 上的点,
上的点,∴
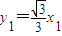 和
和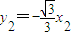 .
.∴
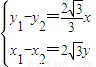 …(4分)
…(4分)又
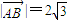 ,∴
,∴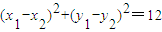 . …(5分)
. …(5分)∴
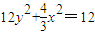 ,∴动点P的轨迹C的方程为
,∴动点P的轨迹C的方程为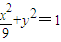 . …(8分)
. …(8分)(2)依题意,直线l的斜率存在,故可设直线l的方程为y=k(x-1).
设M(x3,y3)、N(x4,y4)、R(0,y5),则M、N两点坐标满足方程组
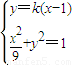
消去y并整理,得(1+9k2)x2-18k2x+9k2-9=0,…(10分)
∴
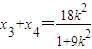 ,①
,①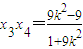 . ②…(12分)
. ②…(12分)∵
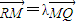 ,∴(x3,y3)-(0,y5)=λ[(1,0)-(x3,y3)].
,∴(x3,y3)-(0,y5)=λ[(1,0)-(x3,y3)].即
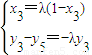 ,∴x3=λ(1-x3).
,∴x3=λ(1-x3).∵l 与x 轴不垂直,∴x3≠1,
∴
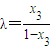 ,同理
,同理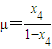 . …(14分)
. …(14分)∴λ+μ=
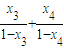 =
=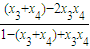 =
=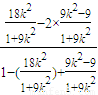 =-
=- .
.∴
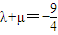 为定值. …(16分)
为定值. …(16分)点评:本题考查动点的轨迹方程,考查直线与椭圆的位置关系,考查向量知识的运用,确定λ、μ的值是关键.

练习册系列答案
相关题目