题目内容
(本小题满分14分)
已知函数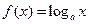 和
和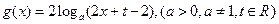 的图象在
的图象在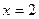 处的切线互相平行.
处的切线互相平行.
(1) 求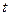 的值;(4分)
的值;(4分)
(2)设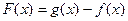 ,当
,当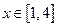 时,
时,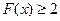 恒成立,求
恒成立,求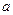 的取值范围. (10分)
的取值范围. (10分)
已知函数
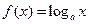 和
和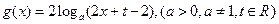 的图象在
的图象在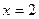 处的切线互相平行.
处的切线互相平行.(1) 求
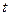 的值;(4分)
的值;(4分)(2)设
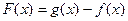 ,当
,当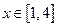 时,
时,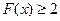 恒成立,求
恒成立,求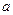 的取值范围. (10分)
的取值范围. (10分)(1)
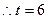
(2)
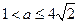
解:(1) 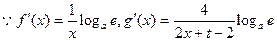 .
.
∵函数 和
和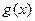 的图象在
的图象在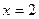 处的切线互相平行,
处的切线互相平行,
 ,
,

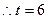 . …4分
. …4分
(2)
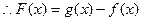

 …6分
…6分
 令
令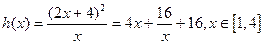
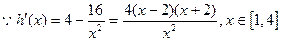 …8分
…8分
∴当 时,
时,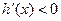 ,当
,当 时,
时,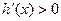 .
.
∴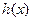 在
在 是单调减函数,在
是单调减函数,在 是单调增函数.
是单调增函数.
 ,
,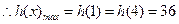 .…10分
.…10分
∴当 时,有
时,有 ,当
,当 时,有
时,有 .
.
∵当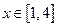 时,
时,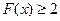 恒成立, ∴
恒成立, ∴
∴满足条件的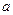 的值满足下列不等式组
的值满足下列不等式组
 ①,或
①,或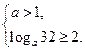 ②…12分
②…12分
不等式组①的解集为空集,解不等式组②得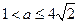 .
.
综上所述,满足条件的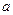 的取值范围是:
的取值范围是: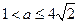 . …14分
. …14分
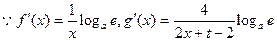 .
. ∵函数
 和
和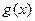 的图象在
的图象在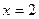 处的切线互相平行,
处的切线互相平行, ,
, 
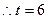 . …4分
. …4分(2)

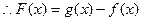

 …6分
…6分 令
令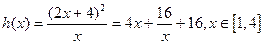
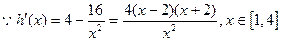 …8分
…8分∴当
 时,
时,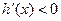 ,当
,当 时,
时,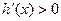 .
.∴
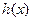 在
在 是单调减函数,在
是单调减函数,在 是单调增函数.
是单调增函数.  ,
,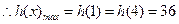 .…10分
.…10分∴当
 时,有
时,有 ,当
,当 时,有
时,有 .
.∵当
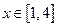 时,
时,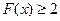 恒成立, ∴
恒成立, ∴
∴满足条件的
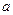 的值满足下列不等式组
的值满足下列不等式组 ①,或
①,或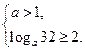 ②…12分
②…12分不等式组①的解集为空集,解不等式组②得
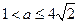 .
.综上所述,满足条件的
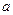 的取值范围是:
的取值范围是: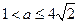 . …14分
. …14分
练习册系列答案
相关题目

 , b=
, b= , C=(
, C=( 则 ( )
则 ( ) ,在函数
,在函数
 的图象上有
的图象上有 、
、 、
、 三点,它们的横坐标分别为
三点,它们的横坐标分别为 、
、 、
、 。
。 的面积为
的面积为 ,求
,求 ;
; 的图象大致是( )
的图象大致是( )

 )的定义域是
)的定义域是 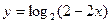 ,若
,若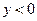 ,则
,则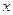 的取值范围是__________
的取值范围是__________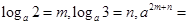
 ,则3n+m的最小值是_______.
,则3n+m的最小值是_______.