题目内容
(理) 空间三点A(0,1,0),B(2,2,0),C(-1,3,1),则
- A.
 与
与 是共线向量
是共线向量 - B.
 的单位向量是(1,1,0)
的单位向量是(1,1,0) - C.
 与
与 夹角的余弦值
夹角的余弦值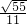
- D.平面ABC的一个法向量是(1,-2,5)
D
分析:A:根据题意两个向量的坐标表示,可得 分别写出
分别写出 ,所以
,所以 不共线.
不共线.
B:结合题意可得: 的单位向量为:
的单位向量为: 或
或 .
.
C:根据题意分别写出两个向量的坐标表示,再结合向量的数量积公式求出两个向量夹角的余弦值.
D:设平面ABC的一个法向量是 ,利用
,利用 ,可得x:y:z=1:(-2):5.
,可得x:y:z=1:(-2):5.
解答:A: =(2,1,0),
=(2,1,0), =(-1,2,1),所以
=(-1,2,1),所以 ,所以
,所以 不共线,所以A错误.
不共线,所以A错误.
B:因为 =(2,1,0),所以
=(2,1,0),所以 的单位向量为:
的单位向量为: 或
或 ,所以B错误.
,所以B错误.
C: =(2,1,0),
=(2,1,0), ,所以cos
,所以cos =
= =-
=-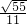 ,所以C错误.
,所以C错误.
D:设平面ABC的一个法向量是 ,因为
,因为 =(2,1,0),
=(2,1,0), =(-1,2,1),所以
=(-1,2,1),所以 ,即
,即 ,所以x:y:z=1:(-2):5,所以D正确.
,所以x:y:z=1:(-2):5,所以D正确.
故选D.
点评:本题主要考查向量之间的运算,即向量坐标形式的数量积运算、向量坐标形式的共线与利用向量的数量积运算求平面的法向量.
分析:A:根据题意两个向量的坐标表示,可得
 分别写出
分别写出 ,所以
,所以 不共线.
不共线.B:结合题意可得:
 的单位向量为:
的单位向量为: 或
或 .
.C:根据题意分别写出两个向量的坐标表示,再结合向量的数量积公式求出两个向量夹角的余弦值.
D:设平面ABC的一个法向量是
 ,利用
,利用 ,可得x:y:z=1:(-2):5.
,可得x:y:z=1:(-2):5.解答:A:
 =(2,1,0),
=(2,1,0), =(-1,2,1),所以
=(-1,2,1),所以 ,所以
,所以 不共线,所以A错误.
不共线,所以A错误.B:因为
 =(2,1,0),所以
=(2,1,0),所以 的单位向量为:
的单位向量为: 或
或 ,所以B错误.
,所以B错误.C:
 =(2,1,0),
=(2,1,0), ,所以cos
,所以cos =
= =-
=-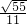 ,所以C错误.
,所以C错误.D:设平面ABC的一个法向量是
 ,因为
,因为 =(2,1,0),
=(2,1,0), =(-1,2,1),所以
=(-1,2,1),所以 ,即
,即 ,所以x:y:z=1:(-2):5,所以D正确.
,所以x:y:z=1:(-2):5,所以D正确.故选D.
点评:本题主要考查向量之间的运算,即向量坐标形式的数量积运算、向量坐标形式的共线与利用向量的数量积运算求平面的法向量.

练习册系列答案
相关题目