Question

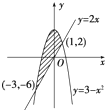
如图中阴影部分的面积是（　　）

• A、2

  3

• B、9-2

  3

• C、

  32

  3

• D、

  35

  3

Answer 1

分析：求阴影部分的面积，先要对阴影部分进行分割到三个象限内，分别对三部分进行积分求和即可．

解答：解：直线y=2x与抛物线y=3-x²
解得交点为（-3，-6）和（1，2）
抛物线y=3-x²与x轴负半轴交点（-

3

，0）
设阴影部分面积为s，则s=

∫

1 0

(3-x2-2x)dx+ 

∫

0 - 3

(3-x2) dx-

∫

0 -3

2xdx+

∫

3 -3

(3-x2) dx
=

5

3

+2

3

+9-2

3

=

32

3

所以阴影部分的面积为

32

3

，
故选C．

点评：本题考查定积分在求面积中的应用，解题是要注意分割，关键是要注意在x轴下方的部分积分为负（积分的几何意义强调代数和），属于基础题．