Question

已知M是正四面体ABCD棱AB的中点，N，E分别是棱CD，BD上的任意点，则下列结论正确的个数有
（1）MN⊥AB；　　　　　　　（2）若N为中点，则MN与AD所成角为45°；
（3）平面CDM⊥平面ABN；　（4）若E为中点，则几何体E-BMN的体积为定值．

1. A.
   1
2. B.
   2
3. C.
   3
4. D.
   4

Answer 1

C
分析：利用线线垂直，线面垂直、面面垂直的位置关系的判定，异面直线夹角的定义、锥体体积公式逐一判断正误，得出正确的个数．
解答：①如图①

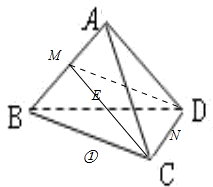
连接MC，MD，由于M是正四面体ABCD棱AB的中点，所以MC⊥AB，MD⊥AB，AB⊥面MCD，MN?面MCD，
∴MN⊥AB． （1）正确．
②如图 ②

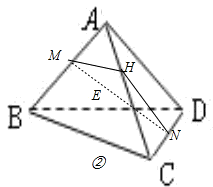
设H为AC中点，
连接HN，MH，则HN∥AD，MH∥BC．
∠HNM即为MN与AD所成角，由（1）已证AB⊥面MCD，
得出AB⊥CD，同理得出AD⊥BC，
∴NH⊥MH，△NHM为等腰直角三角形，∠HNM=45°，
∴MN与AD所成角为45°． （2）正确．
③由（1）已证AB⊥面MCD，AB?面ABN，∴平面CDM⊥平面ABN． （3）正确．
④V _E-BMN=V _M-BEN，M到底面BCD的距离为定值，三角形MEN的面积随N的变化而变化，几何体E-BMN的体积不为定值． （4）错误．
下列结论正确的个数有3个．
故选C．
点评：本题研究了正四面体 的部分性质，考查线线垂直，线面垂直、面面垂直的位置关系的判定，异面直线夹角的定义、锥体体积公式．