题目内容
(本小题满分l2分)
设椭圆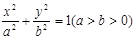 的焦点分别为
的焦点分别为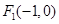 、
、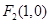 ,直线
,直线 :
: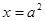 交
交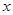 轴于点
轴于点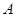 ,且
,且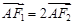 .
.
(1)试求椭圆的方程;
(2)过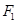 、
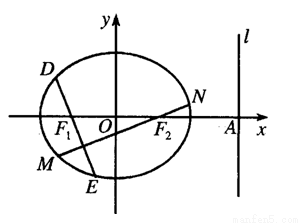
、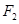 分别作互相垂直的两直线与椭圆分别交于
分别作互相垂直的两直线与椭圆分别交于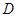 、
、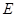 、
、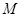 、
、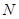 四点(如图所示),试求四边形
四点(如图所示),试求四边形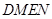 面积的最大值和最小值.
面积的最大值和最小值.
【答案】
(1)椭圆方程为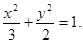
(2)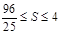 .故四边形
.故四边形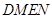 面积的最大值为4,最小值为
面积的最大值为4,最小值为
【解析】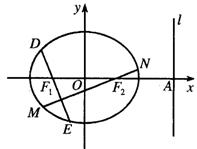 解:(1)由题意,
解:(1)由题意,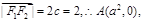
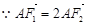
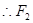 为
为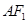 的中点
的中点
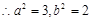
即:椭圆方程为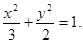 …………………(5分)
…………………(5分)
(2)方法一:当直线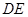 与
与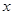 轴垂直时,
轴垂直时,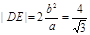 ,此时
,此时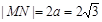 ,四边形
,四边形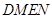 的面积
的面积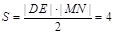 .同理当
.同理当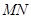 与
与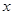 轴垂直时,也有四边形
轴垂直时,也有四边形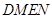 的面积
的面积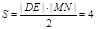 . 当直线
. 当直线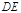 ,
,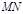 均与
均与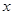 轴不垂直时,设
轴不垂直时,设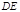 :
: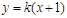 ,代入消去
,代入消去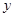 得:
得: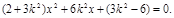 设
设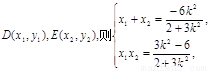 所以,
所以,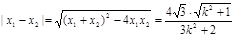 , 所以,
, 所以,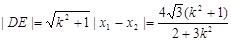 ,同理
,同理 所以四边形的面积
所以四边形的面积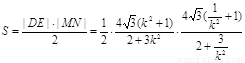
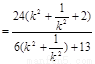
令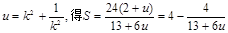 因为
因为 当
当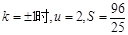 ,且S是以u为自变量的增函数,所以
,且S是以u为自变量的增函数,所以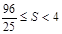 .
.
综上可知,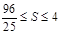 .故四边形
.故四边形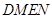 面积的最大值为4,最小值为
面积的最大值为4,最小值为 .…(12分)
.…(12分)
方法二:用直线的参数方程中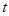 的几何意义.
的几何意义.

练习册系列答案
相关题目
 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式
,求Tn的表达式 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
. :函数
:函数 (
( )的值域是
)的值域是 ;命题
;命题 :指数函数
:指数函数 在
在 上是减函数.若命题“
上是减函数.若命题“ 的范围.
的范围. 并且与曲线
并且与曲线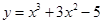 相切的直线方程.
相切的直线方程.