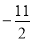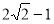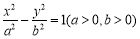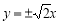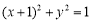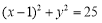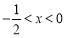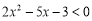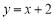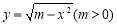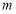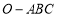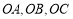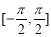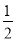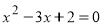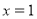题目内容
已知圆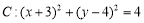 .
.
(1)若直线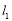 过点
过点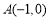 ,且与圆
,且与圆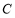 相切,求直线
相切,求直线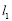 的方程;
的方程;
(2)若圆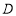 的半径为4,圆心
的半径为4,圆心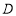 在直线
在直线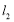 :
: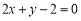 上,且与圆
上,且与圆 内切,求圆
内切,求圆 的方程.
的方程.
(1)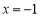 或
或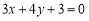 ;(2)
;(2)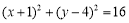 或
或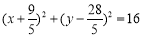 .
.
【解析】
试题分析:(I)由直线l1过定点A(-1,0),故可以设出直线的点斜式方程,然后根据直线与圆相切,圆心到直线的距离等于半径,求出k值即可,但要注意先讨论斜率不存在的情况,以免漏解.
(2)圆D的半径为4,圆心在直线l2:2x+y-2=0上,且与圆C内切,则设圆心D(a,2-2a),进而根据两圆内切,则圆心距等于半径差的绝对值,构造出关于a的方程,解方程即可得到答案.
试题解析:(1)①若直线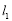 的斜率不存在,直线
的斜率不存在,直线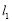 :
: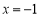 ,符合题意. 2分
,符合题意. 2分
②若直线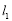 的斜率存在,设直线
的斜率存在,设直线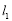 为
为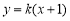 ,即
,即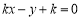 .
.
由题意得, 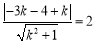 , 4分
, 4分
解得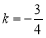 ,∴直线
,∴直线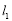 :
: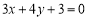 . 7分
. 7分
∴直线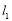 的方程是
的方程是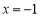 或
或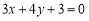 . 8分
. 8分
(2)依题意,设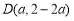 ,
,
由题意得,圆C的圆心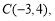 圆C的半径
圆C的半径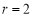 ,
, 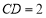 . 12分
. 12分
∴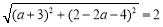 , 解得
, 解得 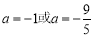 ,
,
∴ 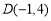 或
或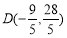 . 14分
. 14分
∴圆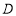 的方程为
的方程为 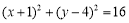 或
或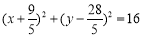 . 16分
. 16分
考点:直线与圆的位置关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目