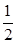题目内容
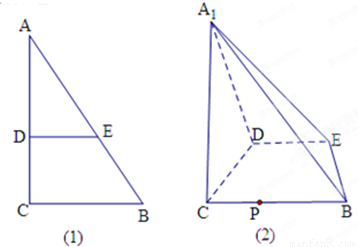
(理)如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).①求直线A1E与平面CBED所成角的正弦值;
②求平面A1CD与平面A1BE所成锐角的余弦值;
③在线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?若存在,求出CP的值;若不存在,请说明理由.

【答案】分析:①建立空间直角坐标系,A1E与平面CBED所成角为θ,确定平面CBED的法向量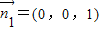 ,
,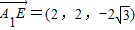 利用向量的夹角公式,即可求直线A1E与平面CBED所成角的正弦值;
利用向量的夹角公式,即可求直线A1E与平面CBED所成角的正弦值;
②求得平面A1CD的法向量为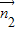 =(1,0,0),平面A1BE的法向量为
=(1,0,0),平面A1BE的法向量为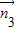 =(2,1,
=(2,1,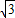 ),利用向量的夹角公式,即可求平面A1CD与平面A1BE所成锐角的余弦值;
),利用向量的夹角公式,即可求平面A1CD与平面A1BE所成锐角的余弦值;
③设线段BC上存在点P,设P点坐标为(0,a,0),则a∈[0,3],求出平面A1DP法向量为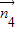 =(-3a,6,
=(-3a,6,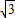 a)假设平面A1DP与平面A1BE垂直,则
a)假设平面A1DP与平面A1BE垂直,则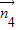 •
•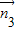 =0,由此可得结论.
=0,由此可得结论.
解答: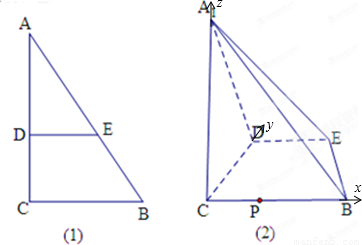 解:由题知DE⊥A1D,DE⊥CD,∴DE⊥平面A1CD,∴DE⊥A1C
解:由题知DE⊥A1D,DE⊥CD,∴DE⊥平面A1CD,∴DE⊥A1C
又BC=3,AC=6,DE∥BC,DE=2,∴A1D=4,CD=2
又A1C⊥CD,∴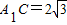 且A1C⊥平面CBED
且A1C⊥平面CBED
以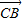 、
、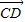 、
、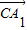 为x、y、z轴的正方向建立空间直角坐标系C-xyz,
为x、y、z轴的正方向建立空间直角坐标系C-xyz,
则C(0,0,0),B(3,0,0),D(0,2,0),E(2,2,0),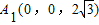
①设A1E与平面CBED所成角为θ
∵平面CBED的法向量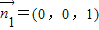 ,
,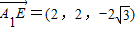
∴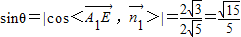
∴A1E与平面CBED所成角的正弦值为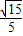 …(7分)
…(7分)
②平面A1CD的法向量为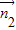 =(1,0,0),
=(1,0,0),
设平面A1BE的法向量为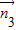 =(x,y,z)
=(x,y,z)
∵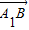 =(3,0,-2
=(3,0,-2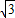 ),
),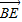 =(-1,2,0)
=(-1,2,0)
∴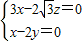 ,∴可取
,∴可取 =(2,1,
=(2,1,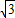 )
)
∴cos<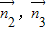 >=
>=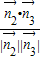 =
=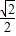
∴平面A1CD与平面A1BE所成锐角的余弦值为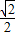
③设线段BC上存在点P,设P点坐标为(0,a,0),则a∈[0,3]
∴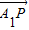 =(0,a,-2
=(0,a,-2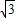 ),
),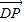 =(2,a,0)
=(2,a,0)
设平面A1DP法向量为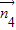 =(x1,y1,z1)
=(x1,y1,z1)
则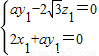 ,∴
,∴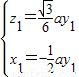
∴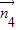 =(-3a,6,
=(-3a,6,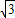 a)
a)
假设平面A1DP与平面A1BE垂直,则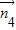 •
•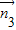 =0,
=0,
∴3a+12+3a=0,∴a=-2
∵0<a<3
∴不存在线段BC上存在点P,使平面A1DP与平面A1BE垂直.
点评:本题考查向量知识的运用,考查线面角、面面角,考查面面垂直,考查学生分析解决问题的能力,属于中档题.
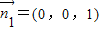 ,
,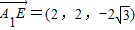 利用向量的夹角公式,即可求直线A1E与平面CBED所成角的正弦值;
利用向量的夹角公式,即可求直线A1E与平面CBED所成角的正弦值;②求得平面A1CD的法向量为
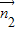 =(1,0,0),平面A1BE的法向量为
=(1,0,0),平面A1BE的法向量为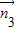 =(2,1,
=(2,1,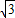 ),利用向量的夹角公式,即可求平面A1CD与平面A1BE所成锐角的余弦值;
),利用向量的夹角公式,即可求平面A1CD与平面A1BE所成锐角的余弦值;③设线段BC上存在点P,设P点坐标为(0,a,0),则a∈[0,3],求出平面A1DP法向量为
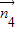 =(-3a,6,
=(-3a,6,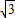 a)假设平面A1DP与平面A1BE垂直,则
a)假设平面A1DP与平面A1BE垂直,则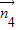 •
•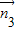 =0,由此可得结论.
=0,由此可得结论.解答:
 解:由题知DE⊥A1D,DE⊥CD,∴DE⊥平面A1CD,∴DE⊥A1C
解:由题知DE⊥A1D,DE⊥CD,∴DE⊥平面A1CD,∴DE⊥A1C又BC=3,AC=6,DE∥BC,DE=2,∴A1D=4,CD=2
又A1C⊥CD,∴
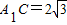 且A1C⊥平面CBED
且A1C⊥平面CBED以
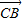 、
、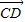 、
、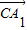 为x、y、z轴的正方向建立空间直角坐标系C-xyz,
为x、y、z轴的正方向建立空间直角坐标系C-xyz,则C(0,0,0),B(3,0,0),D(0,2,0),E(2,2,0),
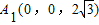
①设A1E与平面CBED所成角为θ
∵平面CBED的法向量
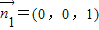 ,
,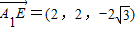
∴
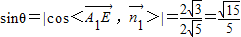
∴A1E与平面CBED所成角的正弦值为
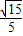 …(7分)
…(7分)②平面A1CD的法向量为
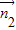 =(1,0,0),
=(1,0,0),设平面A1BE的法向量为
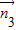 =(x,y,z)
=(x,y,z)∵
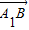 =(3,0,-2
=(3,0,-2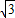 ),
),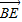 =(-1,2,0)
=(-1,2,0)∴
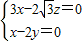 ,∴可取
,∴可取 =(2,1,
=(2,1,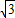 )
)∴cos<
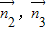 >=
>=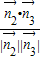 =
=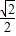
∴平面A1CD与平面A1BE所成锐角的余弦值为
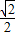
③设线段BC上存在点P,设P点坐标为(0,a,0),则a∈[0,3]
∴
 =(0,a,-2
=(0,a,-2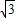 ),
),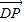 =(2,a,0)
=(2,a,0)设平面A1DP法向量为
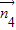 =(x1,y1,z1)
=(x1,y1,z1)则
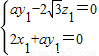 ,∴
,∴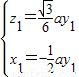
∴
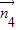 =(-3a,6,
=(-3a,6,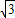 a)
a)假设平面A1DP与平面A1BE垂直,则
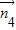 •
•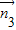 =0,
=0,∴3a+12+3a=0,∴a=-2
∵0<a<3
∴不存在线段BC上存在点P,使平面A1DP与平面A1BE垂直.
点评:本题考查向量知识的运用,考查线面角、面面角,考查面面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
(理)如图5—1,在平行六面体ABCD—A1B1C1D1中,M为AC与BD的交点,
若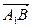 =
=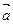 ,
, =
=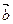 ,
,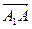 =
= .则下列向量中与
.则下列向量中与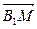 相等的向量是( )
相等的向量是( )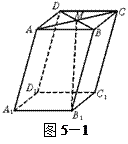

A.-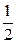 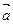 + +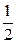 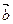 + + | B.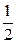 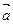 + +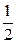 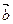 + + |
C.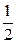 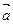 - -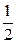 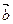 + + | D.-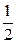 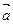 - -  + + |
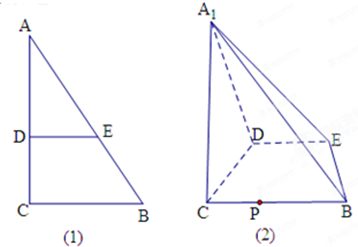 (理)如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).
(理)如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).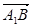 =
=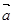 ,
,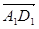 =
=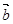 ,
,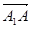 =
=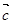 .则下列向量中与
.则下列向量中与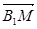 相等的向量是( )
相等的向量是( )