题目内容
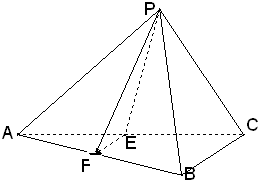 已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.(1)证明EF∥平面PBC.
(2)证明PC⊥平面PAB;
(3)求二面角P-AB-C的平面角的余弦值;
(说明:文科班只做(1),(2)理科班做(1)、(2)、(3))
分析:(1)利用三角形中位线的性质,证明线线平行,从而可得EF∥平面PBC;
(2)连接CF,由△ABC,△PEF是正三角形且E,F为AC、AB的中点,可得PE=EF=
BC=
AC,可得PA⊥PC,由已知易证AB⊥面PCF,从而可得AB⊥PC,利用线面垂直的判定定理可证;
(3)由AB⊥PF,AB⊥CF可得∠PFC为所求的二面角,Rt△PEF中,求解即可.
(2)连接CF,由△ABC,△PEF是正三角形且E,F为AC、AB的中点,可得PE=EF=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由AB⊥PF,AB⊥CF可得∠PFC为所求的二面角,Rt△PEF中,求解即可.
解答:(1)证明:∵E,F是AC,AB的中点,∴EF∥BC,
∵BC?平面PBC,EF?平面PBC
∴EF∥平面PBC;
(2)证明:连结CF.
∵PE=EF=
BC=
AC,
∴AP⊥PC.
∵CF⊥AB,PF⊥AB,
∴AB⊥平面PCF.
∵PC?平面PCF,
∴PC⊥AB,
∴PC⊥平面PAB;
(3)解:∵AB⊥PF,AB⊥CF,
∴∠PFC为所求二面角的平面角.
设AB=a,则AB=a,则PF=EF=
,CF=
a
∴cos∠PFC=
=
.
∵BC?平面PBC,EF?平面PBC
∴EF∥平面PBC;
(2)证明:连结CF.

∵PE=EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴AP⊥PC.
∵CF⊥AB,PF⊥AB,
∴AB⊥平面PCF.
∵PC?平面PCF,
∴PC⊥AB,
∴PC⊥平面PAB;
(3)解:∵AB⊥PF,AB⊥CF,
∴∠PFC为所求二面角的平面角.
设AB=a,则AB=a,则PF=EF=
| a |
| 2 |
| ||
| 2 |
∴cos∠PFC=
| ||||
|
| ||
| 3 |
点评:本小题主要考查空间线面垂直的关系、线面平行、二面角的度量,考查数形结合、化归与转化的数学思想方法,属于中档题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 已知三棱锥P-ABC中,PC⊥底面ABC,AB=BC,D、F分别为AC、PC的中点,DE⊥AP于E.
已知三棱锥P-ABC中,PC⊥底面ABC,AB=BC,D、F分别为AC、PC的中点,DE⊥AP于E. 如图,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB的中点,且△PDB是正三角形,PA⊥PC.
如图,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB的中点,且△PDB是正三角形,PA⊥PC. (2009•河西区二模)如图,已知三棱锥P-ABC中,PA⊥面ABC,其中正视图为Rt△PAC,AC=2
(2009•河西区二模)如图,已知三棱锥P-ABC中,PA⊥面ABC,其中正视图为Rt△PAC,AC=2 (2009•黄浦区二模)已知三棱锥P-ABC的棱长都是2,点D是棱AP上不同于P的点.
(2009•黄浦区二模)已知三棱锥P-ABC的棱长都是2,点D是棱AP上不同于P的点.