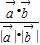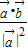题目内容
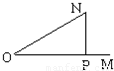
 如图,非零向量
如图,非零向量 | OM |
| a |
| ON |
| b |
| OP |
| a |
分析:由题意可知,向量
与
的数量积等于0,把向量
与
都用向量
与
表示,整理后即可得到λ的值.
| OP |
| PN |
| OP |
| PN |
| a |
| b |
解答:解:由图可知,
•
=0,即λ
•(
-
)=0,
所以λ
•(
-λ
)=λ
•
-λ2|
|2=0,
因为λ≠0,
所以λ=
.
故选C.
| OP |
| PN |
| a |
| ON |
| OP |
所以λ
| a |
| b |
| a |
| a |
| b |
| a |
因为λ≠0,
所以λ=
| ||||
|
|
故选C.
点评:本题考查了平面向量数量积的运算,考查了向量加法的几何意义,解答此题的突破口是运用向量
与
的数量积等于0,此题为中档题.
| OP |
| PN |

练习册系列答案
相关题目
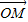 =
=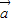 ,
,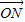 =
=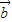 ,且NP⊥OM,P为垂足,若向量
,且NP⊥OM,P为垂足,若向量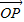 =
=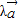 ,则λ的值为( )
,则λ的值为( )