题目内容
经过A(2,0),以(2cosθ-2,sinθ)为方向向量的直线与经过B(-2,0),以(2+2cosθ,sinθ)为方向向量的直线相交于点M(x,y),其中θ≠kπ.(I)求点M(x,y)的轨迹方程;
(II)设(I)中轨迹为曲线C,F1(-
| 3 |
| 3 |
| PF1 |
| PF2 |
分析:(I)根据题意知,
=(2-x,0-y)∥(2cosθ-2,sinθ),根据共线向量定理可得?(x-2)sinθ=y(2cosθ-2),同理(x+2)sinθ=y(2cosθ+2),两式相乘,即可得到点M(x,y)的轨迹方程;
(II)设p(x0,y0)在曲线C内,得
+
<1,再由|PF1|、|OP|、|PF2|成等比数列可得|OP|2=|PF1|•|PF2|?
+
=
•
并代入求得
•
,即可求得结果.
| MA |
(II)设p(x0,y0)在曲线C内,得
| ||
| 4 |
| y | 0 2 |
| x | 0 2 |
| y | 0 2 |
(x0+
|
(x0-
|
并代入求得
| PF1 |
| PF2 |
解答:解:(I)
=(2-x,0-y),(2-x)sinθ+y(2cosθ-2)=0?(x-2)sinθ=y(2cosθ-2)①
同理(-2-x)sinθ+y(2cosθ+2)=0?(x+2)sinθ=y(2cosθ+2)②
①×②得x2-4=-4y2
即
+y2=1;
(II)设p(x0,y0),则
+
<1③
|OP|2=|PF1|•|PF2|?
+
=
•
化简得:
-
=
④
④代入③得0≤
<
1•
2=(-
-x0,-y0)•(
-x0,-y0)=
+
-3=2
-
0≤
<
?-
≤2
-
<-
| MA |
同理(-2-x)sinθ+y(2cosθ+2)=0?(x+2)sinθ=y(2cosθ+2)②
①×②得x2-4=-4y2
即
| x2 |
| 4 |
(II)设p(x0,y0),则
| ||
| 4 |
| y | 2 0 |
|OP|2=|PF1|•|PF2|?
| x | 2 0 |
| y | 2 0 |
(x0+
|
(x0-
|
化简得:
| x | 2 0 |
| y | 2 0 |
| 3 |
| 2 |
④代入③得0≤
| y | 2 0 |
| 1 |
| 2 |
| PF |
| PF |
| 3 |
| 3 |
| x | 2 0 |
| y | 2 0 |
| y | 2 0 |
| 3 |
| 2 |
0≤
| y | 2 0 |
| 1 |
| 2 |
| 3 |
| 2 |
| y | 2 0 |
| 3 |
| 2 |
| 1 |
| 2 |
点评:此题是个中档题.考查向量在几何中的应用,以及数列与解析几何的综合.同时考查学生灵活应用知识分析解决问题的能力.

练习册系列答案
相关题目
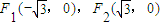 ,若曲线C内存在动点P,使得|PF1|、|OP|、|PF2|成等比数列(O为坐标原点),求
,若曲线C内存在动点P,使得|PF1|、|OP|、|PF2|成等比数列(O为坐标原点),求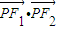 的取值范围.
的取值范围. ,0),F2(
,0),F2( ,0),若曲线C内存在动点P,使得|PF1|、|OP|、|PF2|成等比数列(O为坐标原点),求
,0),若曲线C内存在动点P,使得|PF1|、|OP|、|PF2|成等比数列(O为坐标原点),求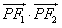 的取值范围。
的取值范围。