题目内容
已知函数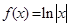
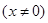 ,函数
,函数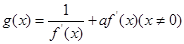
⑴当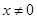 时,求函数
时,求函数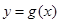 的表达式;
的表达式;
⑵若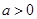 ,函数
,函数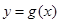 在
在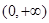 上的最小值是2 ,求
上的最小值是2 ,求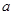 的值;
的值;
⑶在⑵的条件下,求直线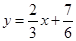
 与函数
与函数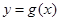 的图象所围成图形的面积.
的图象所围成图形的面积.
【答案】
(1) 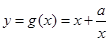 (2)
(2) 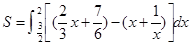 =
=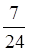 -
2ln2 +ln3
-
2ln2 +ln3
【解析】
导数部分的高考题型主要表现在:利用导数研究函数的性质,高考对这一知识点考查的要求是:理解极大值、极小值、最大值、最小值的概念,并会用导数求函数的单调区间、极大值、极小值及闭区间上的最大值和最小值。⑴∵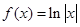 ,∴当
,∴当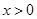 时,
时,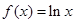 ;
当x<0时,
;
当x<0时,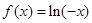 ∴当x>0时,
∴当x>0时,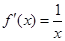 ;
………………2’
;
………………2’
当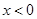 时,
时,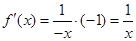
∴当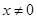 时,函数
时,函数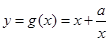 ………………………………………….4’
………………………………………….4’
⑵∵由⑴知当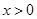 时,
时,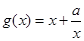 ,…………………………………………………..5’
,…………………………………………………..5’
∴当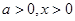 时,
时, 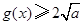 当且仅当
当且仅当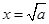 时取等号………………………7’
时取等号………………………7’
∴函数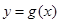 在
在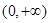 上的最小值是
上的最小值是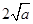 ,∴依题意得
,∴依题意得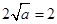 ∴
∴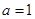 …….8’
…….8’
⑶由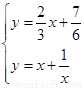 解得
解得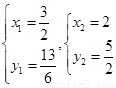 …………………………….10’
…………………………….10’
∴直线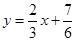 与函数
与函数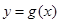 的图象所围成图形的面积
的图象所围成图形的面积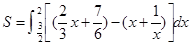 =
=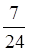 -
2ln2 +ln3
-
2ln2 +ln3

练习册系列答案
相关题目

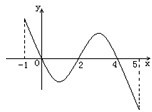 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.给出关于f(x)的下列命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.给出关于f(x)的下列命题: