题目内容
漳州实验中学运动会上甲、乙两班比赛排球,甲班在每局比赛中胜乙班的概率为 ,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.
,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.(1)求前2局甲、乙各胜一局的概率;
(2)求甲班以3:1获胜的概率.
【答案】分析:(1)先前2局甲、乙各胜一局的事件为B,进而分析可得其包括“甲胜第一局,乙胜第二局”与“乙胜第一局,甲胜第二局”两种情况;由互斥事件的概率加法公式计算可得答案;
(2)设甲班以3:1获胜的事件为A,进而分析可得前3局甲班恰好胜2局,然后第4局胜,由相互独立事件的概率与n次独立重复试验中恰有k次发生的概率计算可得答案.
解答:解:(1)设前2局甲、乙各胜一局的事件为B,
分析可得其包括“甲胜第一局,乙胜第二局”与“乙胜第一局,甲胜第二局”两种情况;
则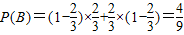 .
.
(2)设甲班以3:1获胜的事件为A.
若甲班以3:1获胜,则前3局甲班恰好胜2局,然后第4局胜.
所以,P(A)=[C32( )2(
)2( )]×
)]× =
=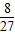 .
.
点评:本题考查相互独立事件的概率、互斥事件的概率以及n次独立重复试验中恰有k次发生的概率;解题的关键在于认清事件所包含的情况.
(2)设甲班以3:1获胜的事件为A,进而分析可得前3局甲班恰好胜2局,然后第4局胜,由相互独立事件的概率与n次独立重复试验中恰有k次发生的概率计算可得答案.
解答:解:(1)设前2局甲、乙各胜一局的事件为B,
分析可得其包括“甲胜第一局,乙胜第二局”与“乙胜第一局,甲胜第二局”两种情况;
则
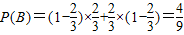 .
.(2)设甲班以3:1获胜的事件为A.
若甲班以3:1获胜,则前3局甲班恰好胜2局,然后第4局胜.
所以,P(A)=[C32(
 )2(
)2( )]×
)]× =
=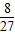 .
.点评:本题考查相互独立事件的概率、互斥事件的概率以及n次独立重复试验中恰有k次发生的概率;解题的关键在于认清事件所包含的情况.

练习册系列答案
相关题目
 ,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.
,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.