题目内容
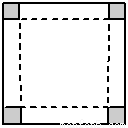
如图,将边长为a的正方形铁皮的四角各截去一个同样大小的小正方形后,将四边向上翻折做成一个无盖的正四棱柱形容器,求此容器的体积最大值.
【答案】
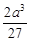
【解析】
试题分析:解:设小正方形的边长为x,则盒底的边长为a-2x,
由于a-2x也要>0,则x∈(0,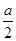 ),
),
且方盒是以边长为a-2x的正方形作底面,高为x的正方体,
其体积为V=x(a-2x)2,(x∈(0,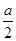 ))
))
V'=(a-2x)(a-6x),令V'=0,则x1= 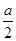 ,x2=
,x2= 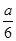 ,
,
由x1=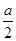 ∉(0,
∉(0,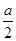 ),且对于x∈(0,
),且对于x∈(0,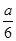 ),V′>0,x∈(
),V′>0,x∈(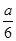 ,
,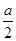 ),V′<0,
),V′<0,
∴函数V在点x=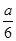 处取得极大值,由于问题的最大值存在,
处取得极大值,由于问题的最大值存在,
∴V(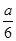 )=
)=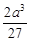
即为容积的最大值.
考点:本题主要考查利用导数知识求函数最值,几何体的特征及体积公式。
点评:本题考查函数的应用,考查函数模型的工具作用,考查求函数最值的导数思想.体现了实际问题数学化的思想,注意发挥导数的工具作用.

练习册系列答案
相关题目
 如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,则正三棱锥的体积是
如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,则正三棱锥的体积是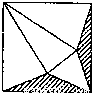 如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,则正三棱锥的体积是 .
如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,则正三棱锥的体积是 .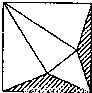 如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,则正三棱锥的体积是 .
如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,则正三棱锥的体积是 .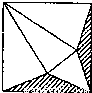 如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,则正三棱锥的体积是 .
如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,则正三棱锥的体积是 .