题目内容
偶函数f(x)的定义域为D={x|x≠0},且满足对于任意x,y∈D,有f(xy)=f(x)+f(y),若x>1时,f(x)>0.
(1)求f(1)的值;
(2)求证f(x)在区间(0,+∞)上是增函数;
(3)若f(4)=1,求不等式f(3x+1)≤2的解集.
解:(1)令x=y=1代入f(xy)=f(x)+f(y),得f(1)=0;
(2)令y= ,代入f(xy)=f(x)+f(y),得f(x)+f(
,代入f(xy)=f(x)+f(y),得f(x)+f( )=0,即f(
)=0,即f( )=-f(x);
)=-f(x);
∵x>1时,f(x)>0,令0<x1<x2, >1,
>1,
∴f( )=f(x2•
)=f(x2• )=f(x2)+f(
)=f(x2)+f( )=f(x2)-f(x1)>0,
)=f(x2)-f(x1)>0,
∴f(x2)>f(x1).
∴f(x)在区间(0,+∞)上是增函数;
(3)∵偶函数f(x)在区间(0,+∞)上是增函数,f(4)=1,
∵f(3x+1)≤2=f(4)+f(4)=f(16),
∴|3x+1|≤16(x≠0),
∴- ≤x<0或0<x≤5.
≤x<0或0<x≤5.
∴所求不等式的解集为:{x|- ≤x<0或0<x≤5}.
≤x<0或0<x≤5}.
分析:(1)令x=y=1代入f(xy)=f(x)+f(y),即可求得f(1)的值;
(2)可令y= ,代入f(xy)=f(x)+f(y),得到f(x)+f(
,代入f(xy)=f(x)+f(y),得到f(x)+f( )=0.再利用函数单调性的定义判断即可;
)=0.再利用函数单调性的定义判断即可;
(3)利用偶函数f(x)在区间(0,+∞)上是增函数,f(4)=1,将不等式f(3x+1)≤2转化为|3x+1|≤16(x≠0),解之即可.
点评:本题考查抽象函数及其用,着重考查函数的单调性,奇偶性及解绝对值不等式,突出考出化归思想与综合分析与应用的能力,属于难题.
(2)令y=
 ,代入f(xy)=f(x)+f(y),得f(x)+f(
,代入f(xy)=f(x)+f(y),得f(x)+f( )=0,即f(
)=0,即f( )=-f(x);
)=-f(x);∵x>1时,f(x)>0,令0<x1<x2,
 >1,
>1,∴f(
 )=f(x2•
)=f(x2• )=f(x2)+f(
)=f(x2)+f( )=f(x2)-f(x1)>0,
)=f(x2)-f(x1)>0,∴f(x2)>f(x1).
∴f(x)在区间(0,+∞)上是增函数;
(3)∵偶函数f(x)在区间(0,+∞)上是增函数,f(4)=1,
∵f(3x+1)≤2=f(4)+f(4)=f(16),
∴|3x+1|≤16(x≠0),
∴-
 ≤x<0或0<x≤5.
≤x<0或0<x≤5.∴所求不等式的解集为:{x|-
 ≤x<0或0<x≤5}.
≤x<0或0<x≤5}.分析:(1)令x=y=1代入f(xy)=f(x)+f(y),即可求得f(1)的值;
(2)可令y=
 ,代入f(xy)=f(x)+f(y),得到f(x)+f(
,代入f(xy)=f(x)+f(y),得到f(x)+f( )=0.再利用函数单调性的定义判断即可;
)=0.再利用函数单调性的定义判断即可;(3)利用偶函数f(x)在区间(0,+∞)上是增函数,f(4)=1,将不等式f(3x+1)≤2转化为|3x+1|≤16(x≠0),解之即可.
点评:本题考查抽象函数及其用,着重考查函数的单调性,奇偶性及解绝对值不等式,突出考出化归思想与综合分析与应用的能力,属于难题.

练习册系列答案
相关题目
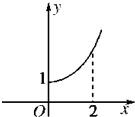 定义在R上的偶函数f(x)的部分图象如图所示,则在(-2,0)上,下列函数中与f(x)的单调性不同的是( )
定义在R上的偶函数f(x)的部分图象如图所示,则在(-2,0)上,下列函数中与f(x)的单调性不同的是( )| A、y=x2+1 | |||||
| B、y=|x|+1 | |||||
C、y=
| |||||
D、y=
|