题目内容
已知f(x)是定义在R上的不恒为零的函数,且对于任意的a,b∈R,满足f=af(b)+bf(a).又已知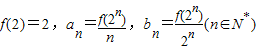 ,考查下列结论:①f(0)=0;②f(-1)=-1;③a2是a1,a3的等比中项;④b2是b1,b3的等差中项.其中正确的是 .(填上所有正确命题的序号)
,考查下列结论:①f(0)=0;②f(-1)=-1;③a2是a1,a3的等比中项;④b2是b1,b3的等差中项.其中正确的是 .(填上所有正确命题的序号)
【答案】分析:令a=b=0,得f(0)=f(0•0)=0,可知①正确;
令a=b=1,得f(1)=f(1•1)=2f(1),f(1)=0;又令a=b=-1,得f(1)=-f(-1)-f(-1)=2f(-1),
得f(-1)=0,可知②不正确;
由f(2)=2,则f(2n)=f(2•2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n,得bn=bn-1+1,{bn}是等差数列,故④正确;
又b1=1,bn=1+(n-1)×1=n,f(2n)=2nbn=n•2n,则an=2n,数列{an}是等比数列,故③正确.
解答:解:∵f(0)=f(0•0)=0•f(0)+0•f(0)=0,∴①正确;
又f(1)=f(1•1)=2f(1),∴f(1)=0;f(1)=f[(-1)•(-1)]=-2f(-1),∴f(-1)=0,故②错;
又∵f(2)=2,∴f(2n)=f(2•2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n,∴bn=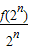 =
=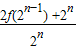 =
=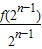 +1
+1
即bn=bn-1+1,∴{bn}是等差数列,故④正确;
又b1=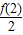 =1,∴bn=1+(n-1)×1=n,∴f(2n)=2nbn=n•2n,∴an=2n,∴数列{an}是等比数列,故③正确.
=1,∴bn=1+(n-1)×1=n,∴f(2n)=2nbn=n•2n,∴an=2n,∴数列{an}是等比数列,故③正确.
故答案为:①③④
点评:本题考查了数列与函数的综合运用,主要涉及了函数的赋值法,等差数列,等比数列的定义及通项公式的计算等知识.
令a=b=1,得f(1)=f(1•1)=2f(1),f(1)=0;又令a=b=-1,得f(1)=-f(-1)-f(-1)=2f(-1),
得f(-1)=0,可知②不正确;
由f(2)=2,则f(2n)=f(2•2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n,得bn=bn-1+1,{bn}是等差数列,故④正确;
又b1=1,bn=1+(n-1)×1=n,f(2n)=2nbn=n•2n,则an=2n,数列{an}是等比数列,故③正确.
解答:解:∵f(0)=f(0•0)=0•f(0)+0•f(0)=0,∴①正确;
又f(1)=f(1•1)=2f(1),∴f(1)=0;f(1)=f[(-1)•(-1)]=-2f(-1),∴f(-1)=0,故②错;
又∵f(2)=2,∴f(2n)=f(2•2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n,∴bn=
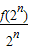 =
=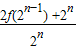 =
=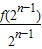 +1
+1即bn=bn-1+1,∴{bn}是等差数列,故④正确;
又b1=
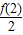 =1,∴bn=1+(n-1)×1=n,∴f(2n)=2nbn=n•2n,∴an=2n,∴数列{an}是等比数列,故③正确.
=1,∴bn=1+(n-1)×1=n,∴f(2n)=2nbn=n•2n,∴an=2n,∴数列{an}是等比数列,故③正确.故答案为:①③④
点评:本题考查了数列与函数的综合运用,主要涉及了函数的赋值法,等差数列,等比数列的定义及通项公式的计算等知识.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目