题目内容
等腰三角形的顶点是A(4,2),底边的一个端点是B(3,5),求另一个端点C的轨迹方程,并说明它的轨迹是什么.
C的轨迹方程是(x-4)2+(y-2)2=10(x≠3,x≠5),
即C的轨迹是以A(4,2)为圆心、10为半径的圆,但除去(3,5)和(5,-1)两点
即C的轨迹是以A(4,2)为圆心、10为半径的圆,但除去(3,5)和(5,-1)两点
设另一端点C的坐标为(x,y).
依题意,得|AC|=|AB|.
由两点间距离公式,得 .
.

整理,得(x-4)2+(y-2)2=10.
这是以点A(4,2)为圆心,以10为半径的圆,如图.
又因为点A,B,C为三角形的三个顶点,所以A,B,C三点不共线,
即有点B,C不能重合.
所以C点的横坐标x≠3.
而且点B,C不能为一直径的两端点,
所以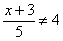 ,点C的横坐标x≠5.
,点C的横坐标x≠5.
故端点C的轨迹方程是(x-4)2+(y-2)2=10(x≠3,x≠5),
即C的轨迹是以A(4,2)为圆心、10为半径的圆,但除去(3,5)和(5,-1)两点.
依题意,得|AC|=|AB|.
由两点间距离公式,得
 .
.
整理,得(x-4)2+(y-2)2=10.
这是以点A(4,2)为圆心,以10为半径的圆,如图.
又因为点A,B,C为三角形的三个顶点,所以A,B,C三点不共线,
即有点B,C不能重合.
所以C点的横坐标x≠3.
而且点B,C不能为一直径的两端点,
所以
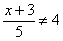 ,点C的横坐标x≠5.
,点C的横坐标x≠5.故端点C的轨迹方程是(x-4)2+(y-2)2=10(x≠3,x≠5),
即C的轨迹是以A(4,2)为圆心、10为半径的圆,但除去(3,5)和(5,-1)两点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目

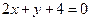 和圆
和圆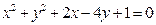 的交点且满足下列条件之一的圆的方程.
的交点且满足下列条件之一的圆的方程.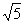
 是圆
是圆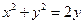 上的动点,求
上的动点,求 的取值范围;
的取值范围;