题目内容
已知0＜α＜
，方程x2sinα+y2cosα=1表示焦点在y轴上的椭圆，则α的取值范围
| π |
| 2 |
(
，
)
| π |
| 4 |
| π |
| 2 |
(
，
)
．| π |
| 4 |
| π |
| 2 |
分析：方程表示焦点在y轴的椭圆，可得x2、y2的分母均为正数，且y2的分母较大，由此建立关于α的不等式．最后结合锐角范围内正弦和余弦的大小关系，解这个不等式，即得α的取值范围．
解答：解：方程x2sinα+y2cosα=1化成标准形式得：
+
=1
．∵方程表示焦点在y轴上的椭圆，
∴
＞
＞0，解之得sinα＞cosα＞0
∵0＜α＜
，
∴
＜α＜
，即α的取值范围是(
，
)
故答案为：(
，
)
| x2 | ||
|
| y2 | ||
|
．∵方程表示焦点在y轴上的椭圆，
∴
| 1 |
| cosα |
| 1 |
| sinα |
∵0＜α＜
| π |
| 2 |
∴
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
故答案为：(
| π |
| 4 |
| π |
| 2 |
点评：本题给出含有字母参数的方程表示椭圆，要我们求参数的取值范围，着重考查了椭圆标准方程和三角函数的大小比较等知识，属于基础题．
练习册系列答案
相关题目
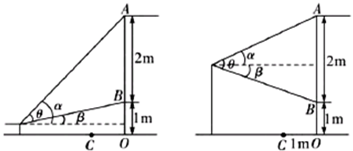国庆长假期间小明去参观画展，为了保护壁画，举办方在壁画前方用垂直于地面的透明玻璃幕墙与观众隔开，小明在一幅壁画正前方驻足观看．如图是小明观看该壁画的纵截面示意图，已知壁画高度AB是2米，壁画底端与地面的距离BO是1米，玻璃幕墙与壁画之间的距离OC是1米．若小明的身高为a米（0＜a＜3），他在壁画正前方x米处观看，问x为多少时，小明观看这幅壁画上下两端所成的视角θ最大？
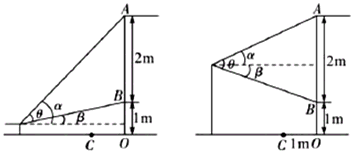国庆长假期间小明去参观画展，为了保护壁画，举办方在壁画前方用垂直于地面的透明玻璃幕墙与观众隔开，小明在一幅壁画正前方驻足观看．如图是小明观看该壁画的纵截面示意图，已知壁画高度AB是2米，壁画底端与地面的距离BO是1米，玻璃幕墙与壁画之间的距离OC是1米．若小明的身高为a米（0＜a＜3），他在壁画正前方x米处观看，问x为多少时，小明观看这幅壁画上下两端所成的视角θ最大？