题目内容
已知异面直线a⊥b，过定点P作直线c，使a与c、b与c所成的角都等于定值φ（45°＜φ＜90°），这样直线c共有（ ）条．
分析：如图所示，过点P分别作PM∥a，PN∥b，三点PMN确定平面α．过点P作PO平分∠MPN．过PO作矩形ABPD⊥平面MPN．
过点D分别作DM⊥PM，DN⊥PN，垂足分别为M，N．连接AM，AN，则PM⊥AM，PN⊥AN，∠APM=∠APN．则直线PA满足条件，同理可找出另一条直线PA′．
过点D分别作DM⊥PM，DN⊥PN，垂足分别为M，N．连接AM，AN，则PM⊥AM，PN⊥AN，∠APM=∠APN．则直线PA满足条件，同理可找出另一条直线PA′．
解答：解：如图所示，过点P分别作PM∥a，PN∥b，三点PMN确定平面α，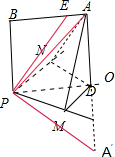
过点P作PO平分∠MPN．过PO作矩形ABPD⊥平面MPN．
过点D分别作DM⊥PM，DN⊥PN，垂足分别为M，N．连接AM，AN，则PM⊥AM，PN⊥AN，
∠APM=∠APN．
则PM=DM，AM=
＞DM=PM，可得90°＞∠APM＞45°．取直线PA为c满足条件，∠APM=∠APN=φ．
同理取点A′与点A关于平面PMN对称，则直线PA′也满足条件．
只有两条直线c满足条件．
故选B．
过点P作PO平分∠MPN．过PO作矩形ABPD⊥平面MPN．
过点D分别作DM⊥PM，DN⊥PN，垂足分别为M，N．连接AM，AN，则PM⊥AM，PN⊥AN，
∠APM=∠APN．
则PM=DM，AM=
| DM2+AD2 |
同理取点A′与点A关于平面PMN对称，则直线PA′也满足条件．
只有两条直线c满足条件．
故选B．
点评：本题考查了利用线面垂直、三垂线定理、异面直线所成的角、直角三角形的边角关系等基础知识与基本技能方法，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
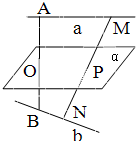已知异面直线a，b的公垂线段AB的中点为O，平面α满足a∥α，b∥α，且O∈α，M、N是a，b上的任意两点，MN∩α=P，求证：P是MN的中点．
，则过空间一定点O，与两条异面直线a,b都成60