题目内容
设集合A={（x，y）|y=ax+1}，B={（x，y）|y=x+b}，且A∩B={（2，5）}，则
- A.a=3，b=2
- B.a=2，b=3
- C.a=-3，b=-2
- D.a=-2，b=-3
B
分析：将交集中的元素分别代入集合A，B，列出方程组求出a，b．
解答：∵A∩B={（2，5）}，
∴
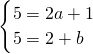
解得a=2，b=3
故选B．
点评：本题考查交集的定义：交集中的元素满足两个集合的公共属性．
分析：将交集中的元素分别代入集合A，B，列出方程组求出a，b．
解答：∵A∩B={（2，5）}，
∴
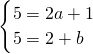
解得a=2，b=3
故选B．
点评：本题考查交集的定义：交集中的元素满足两个集合的公共属性．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
设集合A=B={（x，y）|x∈R，y∈R}，从A到B的映射f：（x，y）→（x+2y，2x-y），则在映射f下B中的元素（1，1）对应的A中元素为（ ）
| A、（1，3） | ||||
| B、（1，1） | ||||
C、(
| ||||
D、(
|
