题目内容
某商场举行购物抽奖促销活动,规定每位顾客从装有编号为0,1,2,3四个相同小球的抽奖箱中,每次取出一球记下编号后放回,连续取两次,若取出的两个小球号码相加之和等于6则中一等奖,等于5中二等奖,等于4或3中三等奖.(1)求中三等奖的概率;
(2)求中奖的概率.
【答案】分析:(1)由题意知本题是一个等可能事件的概率,试验发生包含的事件可以通过列举得到,满足条件的事件从列举出的结果中得到,根据等可能事件的概率公式,得到结果.
(2)本题是一个等可能事件的概率,试验发生包含的事件在前面一问已经做出,满足条件的事件可以列举出所有的结果,根据互斥事件的概率公式和等可能事件的概率公式,得到结果.
解答:解:(1)设“中三等奖”为事件A,“中奖”为事件B,
从四个小球中有放回的取两个共有(0,0),(0,1),(0,2),
(0,3),(1,0),(1,1)(1,2),(1,3),(2,0),
(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3)16种不同的结果
两个小球号码相加之和等于4的取法有3种:(1,3),(2,2),(3,1)
两个小球号相加之和等于3的取法有4种:(0,3),(1,2),(2,1),(3,0)
由互斥事件的加法公式得: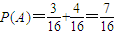 ,
,
即中三等奖的概率为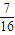 ;
;
(2)两个小球号码相加之和等于3的取法有4种;(0,3),(1,2),(2,1),(3,0)
两个小球相加之和等于4的取法有3种;(1,3),(2,2),(3,1)
两个小球号码相加之和等于5的取法有2种:(2,3),(3,2)
两个小球号码相加之和等于6的取法有1种:(3,3)
由互斥事件的加法公式得:
即中奖的概率为: .
.
点评:本题考查等可能事件的概率,考查互斥事件的概率,是一个同学们都感兴趣的情景问题,是一个基础题.
(2)本题是一个等可能事件的概率,试验发生包含的事件在前面一问已经做出,满足条件的事件可以列举出所有的结果,根据互斥事件的概率公式和等可能事件的概率公式,得到结果.
解答:解:(1)设“中三等奖”为事件A,“中奖”为事件B,
从四个小球中有放回的取两个共有(0,0),(0,1),(0,2),
(0,3),(1,0),(1,1)(1,2),(1,3),(2,0),
(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3)16种不同的结果
两个小球号码相加之和等于4的取法有3种:(1,3),(2,2),(3,1)
两个小球号相加之和等于3的取法有4种:(0,3),(1,2),(2,1),(3,0)
由互斥事件的加法公式得:
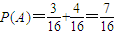 ,
,即中三等奖的概率为
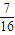 ;
;(2)两个小球号码相加之和等于3的取法有4种;(0,3),(1,2),(2,1),(3,0)
两个小球相加之和等于4的取法有3种;(1,3),(2,2),(3,1)
两个小球号码相加之和等于5的取法有2种:(2,3),(3,2)
两个小球号码相加之和等于6的取法有1种:(3,3)
由互斥事件的加法公式得:

即中奖的概率为:
 .
.点评:本题考查等可能事件的概率,考查互斥事件的概率,是一个同学们都感兴趣的情景问题,是一个基础题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目