题目内容
(本小题满分14分)
如图5, 已知抛物线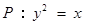 ,直线
,直线 与抛物线
与抛物线 交于
交于 两点,
两点,
 ,
,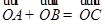 ,
,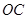 与
与 交于点
交于点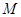 .
.
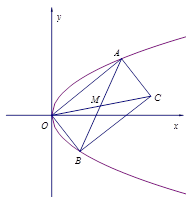
(1)求点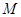 的轨迹方程;
的轨迹方程;
(2)求四边形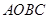 的面积的最小值.
的面积的最小值.
如图5, 已知抛物线
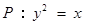 ,直线
,直线 与抛物线
与抛物线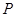 交于
交于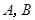 两点,
两点,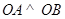 ,
,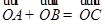 ,
,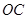 与
与 交于点
交于点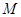 .
.
(1)求点
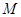 的轨迹方程;
的轨迹方程;(2)求四边形
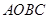 的面积的最小值.
的面积的最小值.(1)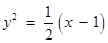 (2)
(2)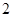
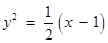 (2)
(2)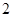
(本小题主要考查抛物线、求曲线的轨迹、均值不等式等基础知识,考查数形结合、函数与方程、化归与转化的数学思想方法,以及推理论证能力、运算求解能力、创新意识)
解法一:
(1)解:设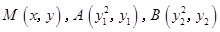 ,
,
∵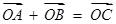 ,
,
∴ 是线段
是线段 的中点. ………… 2分
的中点. ………… 2分
∴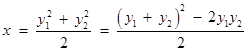 ,① ……… 3分
,① ……… 3分
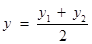 . ② …… 4分
. ② …… 4分
∵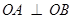 , ∴
, ∴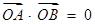 .
.
∴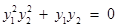 . ……… 5分
. ……… 5分
依题意知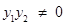 ,
,
∴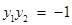 . ③ ………… 6分
. ③ ………… 6分
把②、③代入①得: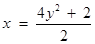 ,即
,即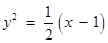 .……… 7分
.……… 7分
∴点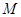 的轨迹方程为
的轨迹方程为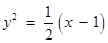 . ………… 8分
. ………… 8分
(2)解:依题意得四边形 是矩形,
是矩形,
∴四边形 的面积为
的面积为
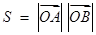
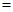
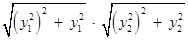 ………… 9分
………… 9分
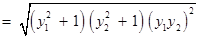
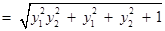
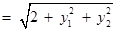 . …… 11分
. …… 11分
∵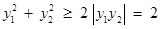 ,当且仅当
,当且仅当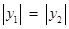 时,等号成立, …………… 12分
时,等号成立, …………… 12分
∴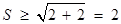 . ………… 13分
. ………… 13分
∴四边形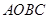 的面积的最小值为
的面积的最小值为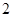 . ……… 14分
. ……… 14分
解法二:
(1)解:依题意,知直线 的斜率存在,设直线
的斜率存在,设直线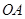 的斜率为
的斜率为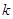 ,
,
由于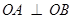 ,则直线
,则直线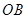 的斜率为
的斜率为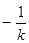 . …………… 1分
. …………… 1分
故直线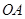 的方程为
的方程为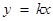 ,直线
,直线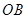 的方程为
的方程为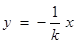 .
.
由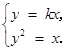 消去
消去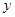 ,得
,得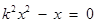 .
.
解得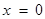 或
或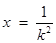 . …………… 2分
. …………… 2分
∴点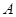 的坐标为
的坐标为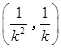 . ……… 3分
. ……… 3分
同理得点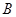 的坐标为
的坐标为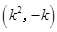 . …… 4分
. …… 4分
∵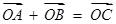 ,
,
∴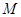 是线段
是线段 的中点. ……… 5分
的中点. ……… 5分
设点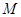 的坐标为
的坐标为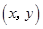 ,
,
则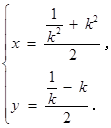 …………… 6分
…………… 6分
消去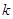 ,得
,得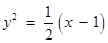 . …………… 7分
. …………… 7分
∴点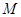 的轨迹方程为
的轨迹方程为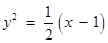 . ……… 8分
. ……… 8分
(2)解:依题意得四边形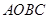 是矩形,
是矩形,
∴四边形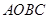 的面积为
的面积为
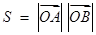
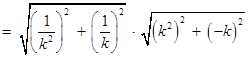 …………… 9分
…………… 9分
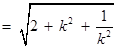 …………… 10分
…………… 10分
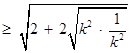 …………… 11分
…………… 11分
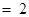 . …………… 12分
. …………… 12分
当且仅当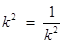 ,即
,即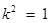 时,等号成立. …………… 13分
时,等号成立. …………… 13分
∴四边形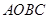 的面积的最小值为
的面积的最小值为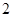 . …………… 14分
. …………… 14分
解法一:
(1)解:设
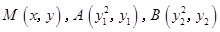 ,
,∵
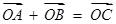 ,
,∴
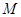 是线段
是线段 的中点. ………… 2分
的中点. ………… 2分∴
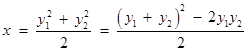 ,① ……… 3分
,① ……… 3分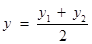 . ② …… 4分
. ② …… 4分∵
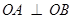 , ∴
, ∴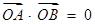 .
.∴
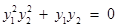 . ……… 5分
. ……… 5分依题意知
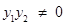 ,
,∴
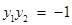 . ③ ………… 6分
. ③ ………… 6分把②、③代入①得:
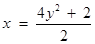 ,即
,即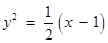 .……… 7分
.……… 7分∴点
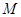 的轨迹方程为
的轨迹方程为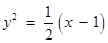 . ………… 8分
. ………… 8分(2)解:依题意得四边形
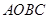 是矩形,
是矩形,∴四边形
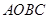 的面积为
的面积为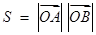
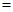
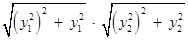 ………… 9分
………… 9分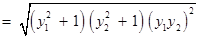
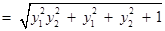
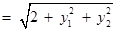 . …… 11分
. …… 11分∵
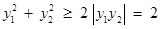 ,当且仅当
,当且仅当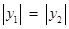 时,等号成立, …………… 12分
时,等号成立, …………… 12分∴
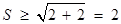 . ………… 13分
. ………… 13分∴四边形
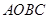 的面积的最小值为
的面积的最小值为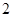 . ……… 14分
. ……… 14分解法二:
(1)解:依题意,知直线
 的斜率存在,设直线
的斜率存在,设直线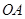 的斜率为
的斜率为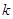 ,
,由于
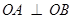 ,则直线
,则直线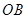 的斜率为
的斜率为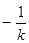 . …………… 1分
. …………… 1分故直线
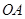 的方程为
的方程为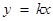 ,直线
,直线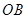 的方程为
的方程为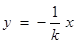 .
.由
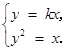 消去
消去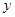 ,得
,得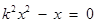 .
.解得
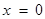 或
或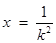 . …………… 2分
. …………… 2分∴点
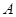 的坐标为
的坐标为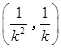 . ……… 3分
. ……… 3分同理得点
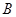 的坐标为
的坐标为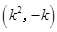 . …… 4分
. …… 4分∵
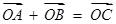 ,
,∴
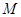 是线段
是线段 的中点. ……… 5分
的中点. ……… 5分设点
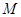 的坐标为
的坐标为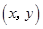 ,
,则
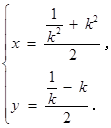 …………… 6分
…………… 6分消去
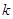 ,得
,得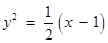 . …………… 7分
. …………… 7分∴点
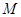 的轨迹方程为
的轨迹方程为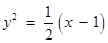 . ……… 8分
. ……… 8分(2)解:依题意得四边形
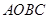 是矩形,
是矩形,∴四边形
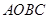 的面积为
的面积为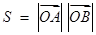
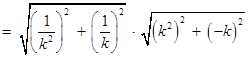 …………… 9分
…………… 9分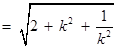 …………… 10分
…………… 10分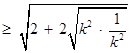 …………… 11分
…………… 11分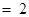 . …………… 12分
. …………… 12分当且仅当
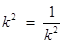 ,即
,即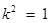 时,等号成立. …………… 13分
时,等号成立. …………… 13分∴四边形
 的面积的最小值为
的面积的最小值为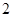 . …………… 14分
. …………… 14分
练习册系列答案
相关题目
 上一点,点
上一点,点 是平面
是平面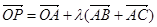 ,若
,若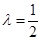 ,则
,则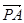 ·
·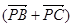 的值等于 .
的值等于 .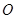 为平面上的定点,
为平面上的定点,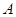 、
、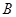 、
、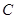 是平面上不共线的三点,若
是平面上不共线的三点,若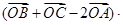
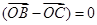 ,则DABC是( )
,则DABC是( )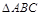 为等边三角形,AB=2,设点P,Q满足
为等边三角形,AB=2,设点P,Q满足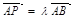 ,
,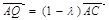
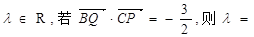
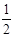
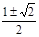
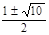
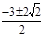
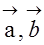 满足
满足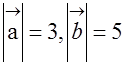 ,
,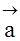 与
与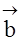 的夹角为
的夹角为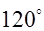 ,则
,则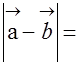 。
。 ,且
,且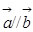 ,则
,则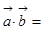 ( )
( )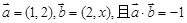 ,则x的值等于( )
,则x的值等于( ) 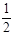
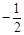
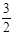
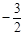
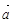 ,
,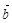 的夹角为
的夹角为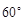 ,且
,且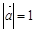 ,则
,则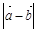 的最小值为
的最小值为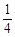
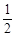
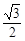
 且
且 与
与 垂直,则实数
垂直,则实数 的值为( )
的值为( )


