题目内容
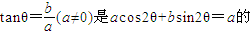 ( )
( )A.充要条件
B.必要不充分条件
C.充分不必要条件
D.即非充分又非必要条件
【答案】分析:先判断p⇒q与q⇒p的真假,再根据充要条件的定义给出结论;也可判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
解答:解:∵acos2θ+bsin2θ=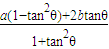
当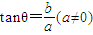 时,acos2θ+bsin2θ=
时,acos2θ+bsin2θ=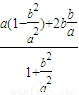 =a
=a
当a=b=0时,acos2θ+bsin2θ=a成立,而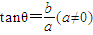 不成立.
不成立.
故,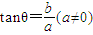 是acos2θ+bsin2θ=a的充分不必要条件
是acos2θ+bsin2θ=a的充分不必要条件
故选C
点评:判断充要条件的方法是:
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
解答:解:∵acos2θ+bsin2θ=
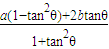
当
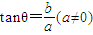 时,acos2θ+bsin2θ=
时,acos2θ+bsin2θ=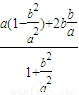 =a
=a当a=b=0时,acos2θ+bsin2θ=a成立,而
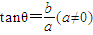 不成立.
不成立.故,
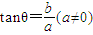 是acos2θ+bsin2θ=a的充分不必要条件
是acos2θ+bsin2θ=a的充分不必要条件故选C
点评:判断充要条件的方法是:
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
在△ABC中,设命题p:
=
=
,命题q:△ABC是等边三角形,那么命题p是命题q的( )
| a |
| sinB |
| b |
| sinC |
| c |
| sinA |
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、即不充分也不必要条件 |