题目内容
已知公比为q(0<q<1)的无穷等比数列{an}各项的和为9,无穷等比数列{an2}各项的和为| 81 | 5 |
(1)求数列{an}的首项a1和公比q;
(2)对给定的k(k=1,2,3,…,n),设数列T(k)是首项为ak,公差为2ak-1的等差数列,求数列T(2)的通项公式及前10项的和.
分析:(1)根据所给的两个无穷等比递缩数列,利用教材中所给的各项之和的公式写出关于首项和公比的方程,解方程即可.
(2)根据第一问做出的结果,写出数列的首项和公差,进而写出数列的通项,求出数列的前10项之和,得到结果.
(2)根据第一问做出的结果,写出数列的首项和公差,进而写出数列的通项,求出数列的前10项之和,得到结果.
解答:解:(1)依题意可知,
?
(2)由(1)知,
数列T(2)的首项为t1=a2=2,公差d=2a2-1=3
T(2)=2+(n-1)×3=3n-1(n∈N*)
S10=10×2+
×10×9×3=155,
即数列T(2)的前10项之和为155.
|
?
|
(2)由(1)知,
数列T(2)的首项为t1=a2=2,公差d=2a2-1=3
T(2)=2+(n-1)×3=3n-1(n∈N*)
S10=10×2+
| 1 |
| 2 |
即数列T(2)的前10项之和为155.
点评:本题是一个数列求和的问题,这种问题在解题时注意看清数列的特征,看出数列是一个特殊数列,可以应用数列的求和公式做出结果,这是求数列的和的题目中比较简单的问题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
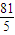 .
.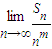 存在且不等于零.
存在且不等于零.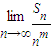 存在且不等于零.
存在且不等于零.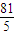 .
.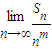 存在且不等于零.
存在且不等于零.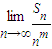 存在且不等于零.
存在且不等于零.