题目内容
已知A(2,3),B(3,0),且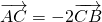 ,则点C的坐标为
,则点C的坐标为
- A.(-3,4)
- B.(4,-3)
- C.

- D.
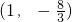
B
分析:由题意A(2,3),B(3,0),且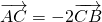 ,设出点C(x,y)的坐标,将向量用坐标表示出来,利用向量相等建立x,y的方程求出x,y的值,即得点C的坐标,选出正确选项
,设出点C(x,y)的坐标,将向量用坐标表示出来,利用向量相等建立x,y的方程求出x,y的值,即得点C的坐标,选出正确选项
解答:设点C(x,y),由于A(2,3),B(3,0),得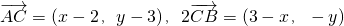 ,
,
又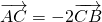
∴-(6-2x,-2y)=(x-2,y-3)
∴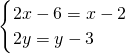 解得
解得 ,即C(4,-3)
,即C(4,-3)
故选B
点评:本题考查向量共线的坐标表示,解题的关键是理解并会运用共线向量坐标表示建立方程求出所引入的参数,向量共线的坐标表示是高考中出现频率较高的一个考点,一般是一个选择题,此类题型很重要,题后要总结做题规律.
分析:由题意A(2,3),B(3,0),且
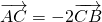 ,设出点C(x,y)的坐标,将向量用坐标表示出来,利用向量相等建立x,y的方程求出x,y的值,即得点C的坐标,选出正确选项
,设出点C(x,y)的坐标,将向量用坐标表示出来,利用向量相等建立x,y的方程求出x,y的值,即得点C的坐标,选出正确选项解答:设点C(x,y),由于A(2,3),B(3,0),得
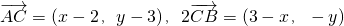 ,
,又
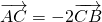
∴-(6-2x,-2y)=(x-2,y-3)
∴
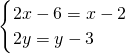 解得
解得 ,即C(4,-3)
,即C(4,-3)故选B
点评:本题考查向量共线的坐标表示,解题的关键是理解并会运用共线向量坐标表示建立方程求出所引入的参数,向量共线的坐标表示是高考中出现频率较高的一个考点,一般是一个选择题,此类题型很重要,题后要总结做题规律.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目