题目内容
在△ABC中,两个定点A(-3,0)B(3,0),△ABC的垂心H(三角形三条高线的交点)是AB边上高线CD的中点.(1)求动点C的轨迹方程;
(2)斜率为2的直线l交动点C的轨迹于P、Q两点,求△OPQ面积的最大值(O是坐标原点).
【答案】分析:(1)设出动点C的坐标,利用AH⊥BC,kAH•kBC=-1即可求解动点C的轨迹方程;
(2)通过斜率为2的直线l,设出直线方程,利用直线交动点C的轨迹于P、Q两点,联立直线与椭圆的方程组成方程组,求出弦长,利用点到直线的距离,表示△OPQ面积,利用基本不等式求出面积的最大值.
解答:解:(1)设动点C(x,y)则D(x,0).因为H是CD的中点,故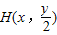
因为AH⊥BC所以kAH•kBC=-1故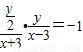
整理得动点C的轨迹方程
(2)设l:y=2x+m并代入 得6x2+4mx+m2-18=0,
得6x2+4mx+m2-18=0,
∵△=(4m)2-4×6×(m2-18)>0
∴54-m2>0
即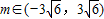 ,
,
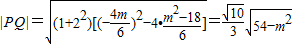
又原点O到直线l的距离为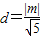
∴S△OPQ= ×
×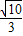 ×
×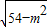 ×
×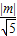 =
=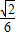
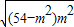 ≤
≤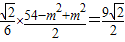
当且仅当54-m2=m2即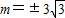 时等号成立,
时等号成立,
故△OPQ面积的最大值为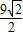 .
.
点评:本题考查曲线轨迹方程的求法,直线与圆锥曲线的关系,弦长公式的应用,点到直线的距离,三角形的面积公式与基本不等式的应用,考查计算能力,转化思想的应用,注意轨迹方程中不满足题意的点需要去掉.
(2)通过斜率为2的直线l,设出直线方程,利用直线交动点C的轨迹于P、Q两点,联立直线与椭圆的方程组成方程组,求出弦长,利用点到直线的距离,表示△OPQ面积,利用基本不等式求出面积的最大值.
解答:解:(1)设动点C(x,y)则D(x,0).因为H是CD的中点,故
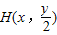
因为AH⊥BC所以kAH•kBC=-1故
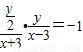
整理得动点C的轨迹方程

(2)设l:y=2x+m并代入
 得6x2+4mx+m2-18=0,
得6x2+4mx+m2-18=0,∵△=(4m)2-4×6×(m2-18)>0
∴54-m2>0
即
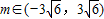 ,
,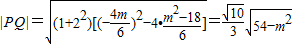
又原点O到直线l的距离为
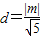
∴S△OPQ=
 ×
×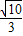 ×
×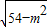 ×
×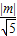 =
=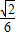
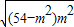 ≤
≤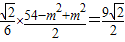
当且仅当54-m2=m2即
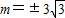 时等号成立,
时等号成立,故△OPQ面积的最大值为
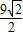 .
.点评:本题考查曲线轨迹方程的求法,直线与圆锥曲线的关系,弦长公式的应用,点到直线的距离,三角形的面积公式与基本不等式的应用,考查计算能力,转化思想的应用,注意轨迹方程中不满足题意的点需要去掉.

练习册系列答案
相关题目