题目内容
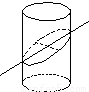
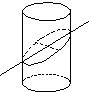 如图所示,一圆柱被与底面成θ(0<θ<
如图所示,一圆柱被与底面成θ(0<θ<| π |
| 2 |
分析:根据平面与圆柱面的截线及椭圆的性质,可设圆柱的底面直径为d,截面与底面成θ,根据截面所得椭圆长轴、短轴与圆柱直径的关系,我们易求出椭圆的长轴长和短轴长,进而得到椭圆的离心率.
解答:解:设圆柱的底面直径为d,截面与底面成θ,
∴椭圆的短轴长2b=d,
椭圆的长轴长2a=
,
根据c=
得,椭圆的半焦距长C=
则椭圆的离心率e=
=
=sinθ.
故选C.
∴椭圆的短轴长2b=d,
椭圆的长轴长2a=
| d |
| cosθ |
根据c=
| a2-b2 |
| d•sinθ |
| 2cosθ |
则椭圆的离心率e=
| c |
| a |
| ||
|
故选C.
点评:若与底面夹角为θ平面α截底面直径为d圆柱,则得到的截面必要椭圆,且椭圆的短轴长等于圆柱的底面直径,长轴长等于
.
| d |
| cosθ |

练习册系列答案
相关题目
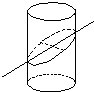 如图所示,一圆柱被与底面成θ(0<θ<
如图所示,一圆柱被与底面成θ(0<θ<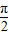 )角的平面所截,其截口是一个椭圆,则这个椭圆的离心率为( )
)角的平面所截,其截口是一个椭圆,则这个椭圆的离心率为( )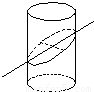
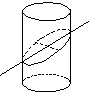 如图所示,一圆柱被与底面成θ(0<θ<
如图所示,一圆柱被与底面成θ(0<θ< )角的平面所截,其截口是一个椭圆,则这个椭圆的离心率为
)角的平面所截,其截口是一个椭圆,则这个椭圆的离心率为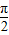 )角的平面所截,其截口是一个椭圆,则这个椭圆的离心率为( )
)角的平面所截,其截口是一个椭圆,则这个椭圆的离心率为( )