题目内容
已知椭圆C的中心在原点,焦点在x轴上,离心率为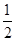 ,短轴长为4
,短轴长为4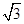 .
.
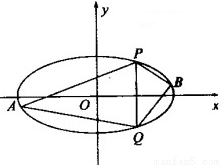
(I)求椭圆C的标准方程;
(II)直线x=2与椭圆C交于P、Q两点,A、B是椭圆O上位于直线PQ两侧的动点,且直线AB的斜率为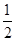 .
.
①求四边形APBQ面积的最大值;
②设直线PA的斜率为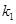 ,直线PB的斜率为
,直线PB的斜率为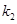 ,判断
,判断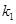 +
+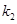 的值是否为常数,并说明理由.
的值是否为常数,并说明理由.
【答案】
(1)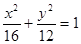
(2)故当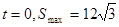 ,
,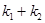 的值为常数0.
的值为常数0.
【解析】
试题分析:解:(Ⅰ)设椭圆C的方程为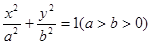 .
1分
.
1分
由已知b=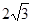 离心率
离心率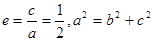 ,得
,得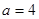
所以,椭圆C的方程为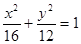 .
4分
.
4分
(Ⅱ)①由(Ⅰ)可求得点P、Q的坐标为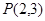 ,
,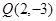 ,则
,则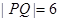 , 5分
, 5分
设A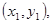 B(
B(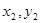 ),直线AB的方程为
),直线AB的方程为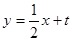 ,代人
,代人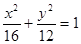
得: .
.
由△>0,解得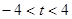 ,由根与系数的关系得
,由根与系数的关系得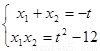 7分
7分
四边形APBQ的面积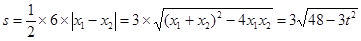
故当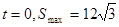 …②由题意知,直线PA的斜率
…②由题意知,直线PA的斜率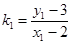 ,直线PB的斜率
,直线PB的斜率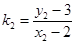
则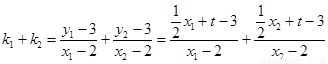 10分
10分
=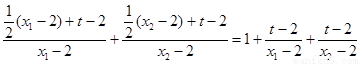
=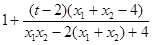 ,由①知
,由①知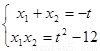
可得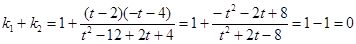
所以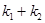 的值为常数0.
13分
的值为常数0.
13分
考点:直线与椭圆的位置关系
点评:主要是考查了直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
相关题目

 。
。