题目内容
.圆 的方程为
的方程为 ,圆
,圆 的方程为
的方程为
 ,过圆
,过圆 上任意一点
上任意一点 作圆
作圆 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 、
、 ,则
,则 的最小值是( )
的最小值是( )
A.6
B.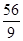 C.7 D.
C.7 D.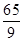
【答案】
B
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
.圆 的方程为
的方程为 ,圆
,圆 的方程为
的方程为
 ,过圆
,过圆 上任意一点
上任意一点 作圆
作圆 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 、
、 ,则
,则 的最小值是( )
的最小值是( )
A.6
B.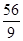 C.7 D.
C.7 D.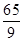
B
【解析】略

 阅读快车系列答案
阅读快车系列答案