题目内容
已知函数f(x)=asin(πx+α)+bcos(πx+β),其中a,b,α,β都是非零实数且满足f(2013)=-1,则f(2014)=________.
1
由已知条件,得
f(2013)=asin(2013π+α)+bcos(2013π+β)
=asin(π+α)+bcos(π+β)
=-asinα-bcosβ
=-1,
∴asinα+bcosβ=1.
而f(2014)=asin(2014π+α)+bcos(2014π+β)
=asinα+bcosβ
=1.
f(2013)=asin(2013π+α)+bcos(2013π+β)
=asin(π+α)+bcos(π+β)
=-asinα-bcosβ
=-1,
∴asinα+bcosβ=1.
而f(2014)=asin(2014π+α)+bcos(2014π+β)
=asinα+bcosβ
=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
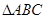 的内角
的内角 ,
, ,
, 的对边分别是
的对边分别是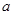 ,
,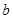 ,
,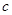 ,若
,若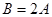 ,
,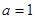 ,
,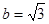 ,则
,则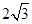
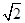
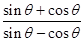 =2,则sin(θ-5π)sin
=2,则sin(θ-5π)sin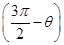 =________.
=________. ,
,

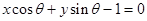 与圆
与圆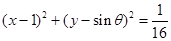 相切,且
相切,且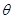 为锐角,则这条直线的斜率是( )
为锐角,则这条直线的斜率是( )



 的值为( ).
的值为( ).




 ,则
,则 .
.