题目内容
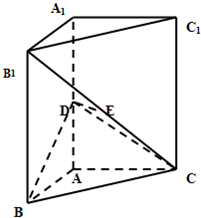 如图,直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC,D、E分别为AA1、B1C的中点.
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC,D、E分别为AA1、B1C的中点.(I)证明:DE∥底面ABC
(II)设二面角A-BC-D为60°;求BD与平面BCC1B1所成的角的正弦值.
分析:(I)取BC的中点F,连接EF,DF,BE,先根据E为B1C的中点得到EF=DA,EF∥DA进而得AFED为平行四边形;即可得到DE∥底面ABC.
(II)先根据第一问的结论知道∠DBE即为BD与平面BCC1B1所成的角;再结合∠DAF即为二面角A-BC-D的平面角求出边长即可求出结论.
(II)先根据第一问的结论知道∠DBE即为BD与平面BCC1B1所成的角;再结合∠DAF即为二面角A-BC-D的平面角求出边长即可求出结论.
解答: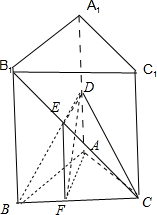 (I)证:取BC的中点F,连接EF,DF,BE,
(I)证:取BC的中点F,连接EF,DF,BE,
∵AB=AC,∴AF⊥BC,
因为E为B1C的中点
∴EF∥BB1,FE=
BB1,
∴EF=DA,EF∥DA
∴AFED为平行四边形,
∴DE∥AF,
∴DE∥平面ABC.
(II)解:∵AF⊥BC,AF⊥BB1,
∴AF⊥平面BCC1B1,
∵DE∥AF⇒DE⊥平面BCC1B1
∴∠DBE即为BD与平面BCC1B1所成的角.
∵二面角A-BC-D为60°;
而DA⊥平面ABC,AF⊥BC;
∴∠DAF即为二面角A-BC-D的平面角,
所以∠DAF=60°,tan∠DFA=
⇒DF=AF•tan∠DFA=
×tan60°=
.
∴BD=
=
=
.
∴sin∠DBE=
=
=
=
.
即BD与平面BCC1B1所成的角的正弦值为:
.
 (I)证:取BC的中点F,连接EF,DF,BE,
(I)证:取BC的中点F,连接EF,DF,BE,∵AB=AC,∴AF⊥BC,
因为E为B1C的中点
∴EF∥BB1,FE=
| 1 |
| 2 |
∴EF=DA,EF∥DA
∴AFED为平行四边形,
∴DE∥AF,
∴DE∥平面ABC.
(II)解:∵AF⊥BC,AF⊥BB1,
∴AF⊥平面BCC1B1,
∵DE∥AF⇒DE⊥平面BCC1B1
∴∠DBE即为BD与平面BCC1B1所成的角.
∵二面角A-BC-D为60°;
而DA⊥平面ABC,AF⊥BC;
∴∠DAF即为二面角A-BC-D的平面角,
所以∠DAF=60°,tan∠DFA=
| DA |
| AF |
| ||
| 2 |
| ||
| 2 |
∴BD=
| DE 2+AB 2 |
(
|
| ||
| 2 |
∴sin∠DBE=
| DE |
| BD |
| AF |
| BD |
| ||||
|
| ||
| 5 |
即BD与平面BCC1B1所成的角的正弦值为:
| ||
| 5 |
点评:本题主要考察线面所成的角以及线面平行的判定.一般在证明线面平行时,常转化为证线线平行.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.