题目内容
定义一种新运算:a•b=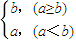 已知函数f(x)=(1+
已知函数f(x)=(1+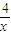 )•log2x,若函数g(x)=f(x)-k恰有两个零点,则k的取值范围为( )
)•log2x,若函数g(x)=f(x)-k恰有两个零点,则k的取值范围为( )A.(1,2]
B.(1,2)
C.(0,2)
D.(0,1)
【答案】分析:由新定义可得函数f(x)的解析式,问题等价于函数f(x)与y=k的图象有两个交点,作出函数的图象可得答案.
解答: 解:令1+
解:令1+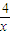 =log2x,可解得x=4,此时函数值为2,
=log2x,可解得x=4,此时函数值为2,
而且当0<x≤4时,1+ ≥log2x,当x>4时1+
≥log2x,当x>4时1+ <log2x,
<log2x,
故f(x)=(1+ )•log2x=
)•log2x= ,
,
函数g(x)=f(x)-k恰有两个零点等价于
函数f(x)与y=k的图象有两个交点,
作出函数的图象:
由图象可知,k的取值范围为(1,2)
故选B
点评:本题考查根的存在性即个数的判断,数形结合是解决问题的关键,属中档题.
解答:
 解:令1+
解:令1+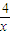 =log2x,可解得x=4,此时函数值为2,
=log2x,可解得x=4,此时函数值为2,而且当0<x≤4时,1+
 ≥log2x,当x>4时1+
≥log2x,当x>4时1+ <log2x,
<log2x,故f(x)=(1+
 )•log2x=
)•log2x= ,
,函数g(x)=f(x)-k恰有两个零点等价于
函数f(x)与y=k的图象有两个交点,
作出函数的图象:
由图象可知,k的取值范围为(1,2)
故选B
点评:本题考查根的存在性即个数的判断,数形结合是解决问题的关键,属中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
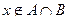 },又已知A={0,1,2,},B={1,2,3
},又已知A={0,1,2,},B={1,2,3 },用列举法写出A*B=
},用列举法写出A*B=