题目内容
已知1,x1,x2,7成等差数列,1,y1,y2,8成等比数列,点M(x1,y1),N(x2,y2),则线段MN的中垂线方程是
x+y-7=0
x+y-7=0
.分析:根据等差数列和等比数列的性质可分别求出公差和公比,进而得出x1,x2,y1,y2的值,从而可知MN中点坐标和中垂线的斜率,最后由点斜式求出方程.
解答:解:∵1,x1,x2,7成等差数列,
∴d=
=2
∴x1=1+2=3,x2=1+4=5
又∵1,y1,y2,8成等比数列,
∴q=2
∴y1=1×2=2,y2=1×4=4,
则 M(3,2),N(5,4),
∴MN中点为(4,3),kMN=
=1,
∴MN的中垂线方程为y-3=-(x-4),即x+y-7=0.
故答案为:x+y-7=0.
∴d=
| 7-1 |
| 4-1 |
∴x1=1+2=3,x2=1+4=5
又∵1,y1,y2,8成等比数列,
∴q=2
∴y1=1×2=2,y2=1×4=4,
则 M(3,2),N(5,4),
∴MN中点为(4,3),kMN=
| 4-2 |
| 5-3 |
∴MN的中垂线方程为y-3=-(x-4),即x+y-7=0.
故答案为:x+y-7=0.
点评:本题考查等差数列和等比数列的性质,要求对等差数列、等比数列的性质牢固掌握.属简单题

练习册系列答案
相关题目
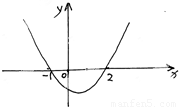
 如图所示为二次函数f(x)的图象,已知-1<x1<x2<2,那么(x1+1)f(x2)-(x2+1)f(x1)为( )
如图所示为二次函数f(x)的图象,已知-1<x1<x2<2,那么(x1+1)f(x2)-(x2+1)f(x1)为( )