题目内容
已知点A（4，16），点P是双曲线C：x2-| y2 | 15 |
分析：先根据双曲线的方程求得c，求得F的坐标，进而看当A，F，P不共线时根据三角形三边的关系可推断出|PA|+|PF|＞|AF|，进而可推断出|PA|+|PF|≥|AF|，利用两点间的距离公式求得|AF|答案可得．
解答：解：根据双曲线的方程可求得c=
=4，
当A，F，P不共线时根据三角形三边的关系可知|PA|+|PF|＞|AF|
当A，F，P共线时|AF|=
=16
∴|PA|+|PF|≥|AF|=16
故答案为：16
| 1+15 |
当A，F，P不共线时根据三角形三边的关系可知|PA|+|PF|＞|AF|
当A，F，P共线时|AF|=
| 0+256 |
∴|PA|+|PF|≥|AF|=16
故答案为：16
点评：本题主要考查了双曲线的简单性质．考查了学生数形结合思想的运用和分析推理能力．
练习册系列答案
阅读快车系列答案
相关题目
已知点A（2，-3）、B（-3，-2），直线l：λx-4y+4-λ=0与线段AB恒有公共点，则λ的取值范围是（ ）
| A、λ≥3或λ≤-16 | ||
B、λ≥
| ||
| C、-16≤λ≤3 | ||
| D、3≤λ≤16 |
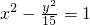上的一个动点，点F是双曲线C的右焦点，则|PA|+|PF|的最小值为________．