题目内容
设奇函数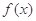 在
在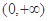 上为增函数,且
上为增函数,且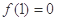 ,则不等式
,则不等式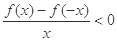 的解集为( )
的解集为( )
A.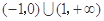 B.
B.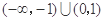
C.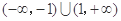 D.
D.
【答案】
D
【解析】
试题分析:首先利用奇函数定义与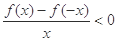 得出x与f(x)异号,然后由奇函数定义求出f(-1)=-f(1)=0,最后结合f(x)的单调性解出答案.解:由奇函数f(x)可知
得出x与f(x)异号,然后由奇函数定义求出f(-1)=-f(1)=0,最后结合f(x)的单调性解出答案.解:由奇函数f(x)可知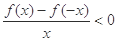 即x与
即x与
f(x)异号,而f(1)=0,则f(-1)=-f(1)=0,又f(x)在(0,+∞)上为增函数,则奇函数f(x)
在(-∞,0)上也为增函数,当x>0时,f(x)<0=f(1);当x<0时,f(x)>0=f(-1),所以0<x
<1或-1<x<0.故选D.
考点:奇函数和单调性的运用
点评:本题综合考查奇函数定义与它的单调性.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 在
在 上为增函数,且
上为增函数,且 ,则不等式
,则不等式 的解集为 .
的解集为 . 在
在 上为增函数,且
上为增函数,且 ,则不等式
,则不等式 的解集为( )
的解集为( ) B.
B. C.
C. D.
D.
 在
在 上为增函数,且
上为增函数,且 ,则不等式
,则不等式 的解集为( )
的解集为( ) B.
B.  C.
C.  D.
D. 