题目内容
设a、b、c是三个向量,且a∥b,b∥c,则
- A.a∥c总是成立的
- B.当a≠0时,a∥c
- C.当b≠0时,a∥c
- D.当c≠0时,a∥c
C
以分析选项A:当b=0时,a∥b与b∥c都成立,但此时a与c可能平行,也可能不平行.所以,选项A不正确.分析选项B和选项D:例如,a与c的方向一个是正北方向一个是正东方向,且a≠0,c≠0,b=0,这时a∥b与b∥c都成立,但a∥c不成立.所以,选项B、D都不正确.论证选项C的正确性:当b≠0时,若a、c中至少有一个是0,则a∥c若a≠0,c≠0,则a∥b表明a与b同向或反向,b∥c表明b与c同向或反向,所以,a与c同向或反向,即a∥c.)
以分析选项A:当b=0时,a∥b与b∥c都成立,但此时a与c可能平行,也可能不平行.所以,选项A不正确.分析选项B和选项D:例如,a与c的方向一个是正北方向一个是正东方向,且a≠0,c≠0,b=0,这时a∥b与b∥c都成立,但a∥c不成立.所以,选项B、D都不正确.论证选项C的正确性:当b≠0时,若a、c中至少有一个是0,则a∥c若a≠0,c≠0,则a∥b表明a与b同向或反向,b∥c表明b与c同向或反向,所以,a与c同向或反向,即a∥c.)

练习册系列答案
相关题目
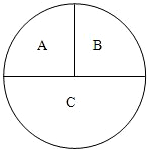 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.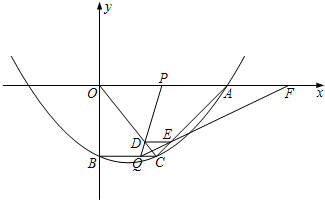 如图,在平面直角坐标系xoy中,抛物线y=
如图,在平面直角坐标系xoy中,抛物线y=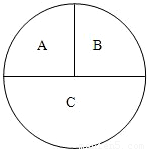 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.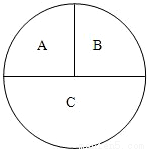 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.