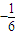题目内容
如图，已知点O是边长为1的等边△ABC的中心，则（| OA |
| OB |
| OA |
| OC |
分析：由题意求出|
|，|
|， |
|的长度，推出夹角大小，直接利用向量的数量积求解即可．
| OA |
| OB |
| OC |
解答：解：因为点O是边长为1的等边△ABC的中心，D为BC的中点，
，
，
两两夹角为120°．
所以|
|=|
|=|
|=
|AD|=
×
=
．
所以（
+
）•（
+
）
=
2+
•
+
•
+
•
=(
)2+(
)2cos120°+(
)2cos120°+(
)2cos120°
=(
)2(1+3cos120°)
=-
．
故选D．
| OA |
| OC |
| OB |
所以|
| OA |
| OB |
| OC |
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
所以（
| OA |
| OB |
| OA |
| OC |
=
| OA |
| OB |
| OA |
| OA |
| OC |
| OB |
| OC |
=(
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
=(
| ||
| 3 |
=-
| 1 |
| 6 |
故选D．
点评：本题考查向量的数量积的运算，利用条件求出|
|=|
|=|
|的值，已经向量的夹角是解题的关键．
| OA |
| OB |
| OC |
练习册系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
)·(
)等于
B．
C．
D．
)·(
)等于
B．
C．
D．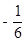
）•（
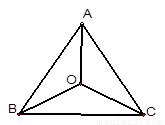
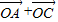）等于（ ）
）•（
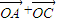）等于（ ）
