题目内容
设α、β都是锐角,且cosα=
,sin(α+β)=
,则cosβ( )
| ||
| 5 |
| 3 |
| 5 |
A.
| B.
| C.
| D.
|
∵α、β都是锐角,且cosα=
<
,
∴
<α<
,又sin(α+β)=
>
,
∴
<α+β<π,
∴cos(α+β)=-
=-
,sinα=
=
,
则cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-
×
+
×
=
.
故选A
| ||
| 5 |
| 1 |
| 2 |
∴
| π |
| 3 |
| π |
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
∴
| π |
| 2 |
∴cos(α+β)=-
| 1-sin2(α+β) |
| 4 |
| 5 |
| 1-cos2α |
2
| ||
| 5 |
则cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-
| 4 |
| 5 |
| ||
| 5 |
| 3 |
| 5 |
2
| ||
| 5 |
2
| ||
| 25 |
故选A

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
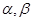 都是锐角,且
都是锐角,且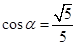 ,
,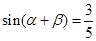 则
则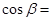 ( )
( )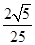 B.
B.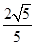 C.
C.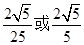 D.
D.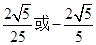
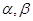 都是锐角,且
都是锐角,且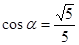 ,
,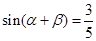 ,则
,则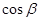 =( )
=( )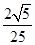 B.
B.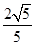 C.
C.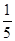 或
或