题目内容
定义函数集合M={f(x)|f′(x)>0},N={f(x)|f″(x)>0},(其中f′(x)为f(x)的导函数,f″(x)为f′(x)的导函数),D=M∩N,以下5个函数中 ①f(x)=ex,②f(x)=lnx,③f(x)=x-2,x∈(-∞,0),④f(x)=x+
,x∈(1,+∞),⑤f(x)=cosx,x∈(o,
) 属于集合D的有( )
| 1 |
| x |
| π |
| 2 |
分析:根据题目给出的集合D的定义,知道集合D中的元素应是导函数和导函数的导函数都在给定的定义域内为正值的函数,对5个函数逐一进行判断就可得到答案.
解答:解:由函数集合M={f(x)|f′(x)>o},N={f(x)|f″(x)>0},(其中f′(x)为f(x)的导函数,f″(x)为f′(x)的导函数),D=M∩N,
知集合D中的元素是f′(x)与f′′(x)均大于0的f(x)构成,
对于f(x)=ex,f′(x)=f′′(x)=ex>0,满足题意,所以①是集合D中的元素;
对于f(x)=lnx,因为x>0,所以f′(x)=
>0,f′′(x)=(
)′=-
<0,所以②不合题意;
对于f(x)=x-2,x∈(-∞,0),f′(x)=-2x-3>0,f′′(x)=(-2x-3)′=6x-4>0,所以③是集合D中的元素;
对于f(x)=x+
,x∈(1,+∞),f′(x)=(x+
)′=1-
>0,f′′(x)=(1-
)′=
>0,所以④是集合D中的元素;
对于f(x)=cosx,x∈(o,
),f′(x)=(cosx)′=-sinx<0,所以,⑤不合题意.
故选D.
知集合D中的元素是f′(x)与f′′(x)均大于0的f(x)构成,
对于f(x)=ex,f′(x)=f′′(x)=ex>0,满足题意,所以①是集合D中的元素;
对于f(x)=lnx,因为x>0,所以f′(x)=
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
对于f(x)=x-2,x∈(-∞,0),f′(x)=-2x-3>0,f′′(x)=(-2x-3)′=6x-4>0,所以③是集合D中的元素;
对于f(x)=x+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x2 |
| 2 |
| x3 |
对于f(x)=cosx,x∈(o,
| π |
| 2 |
故选D.
点评:本题考查了导数的运算及元素与集合关系的判断,是新定义题,解答此题的关键是熟记基本初等函数的求导公式及导数的运算法则,同时掌握简单的复合函数的求导运算.

练习册系列答案
相关题目
 ,x∈(1,+∞),⑤f(x)=cosx,x
,x∈(1,+∞),⑤f(x)=cosx,x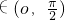 属于集合D的有
属于集合D的有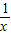 ,x∈(1,+∞),⑤f(x)=cosx,x
,x∈(1,+∞),⑤f(x)=cosx,x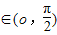 属于集合D的有( )
属于集合D的有( )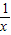 ,x∈(1,+∞),⑤f(x)=cosx,x
,x∈(1,+∞),⑤f(x)=cosx,x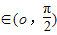 属于集合D的有( )
属于集合D的有( )