题目内容
已知数列{an}中,a1=1,当n≥2时,其前n项和Sn满足S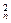 =an(Sn-
=an(Sn-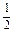 ).
).
(1)证明: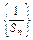 是等差数列,求Sn的表达式;
是等差数列,求Sn的表达式;
(2)设bn=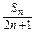 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.
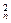 =an(Sn-
=an(Sn-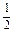 ).
).(1)证明:
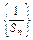 是等差数列,求Sn的表达式;
是等差数列,求Sn的表达式;(2)设bn=
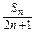 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.(1)略
(2)
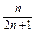
解 (1)∵S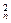 =an
=an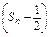 ,an=Sn-Sn-1(n≥2),
,an=Sn-Sn-1(n≥2),
∴S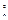 =(Sn-Sn-1)
=(Sn-Sn-1)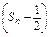 , 2Sn-1Sn=Sn-1-Sn, ① ---------2分
, 2Sn-1Sn=Sn-1-Sn, ① ---------2分
由题意Sn-1·S n≠0,①式两边同除以Sn-1·Sn ,得
n≠0,①式两边同除以Sn-1·Sn ,得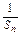 -
-
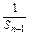 =2,------4分
=2,------4分
∴数列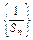 是首项为
是首项为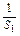 =
=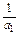 =1,公差为2的等差数列.
=1,公差为2的等差数列.
∴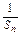 =1+2(n-1)=2n-1, --------5分
=1+2(n-1)=2n-1, --------5分
∴Sn=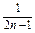 . ------6分
. ------6分
(2)又bn=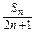 =
=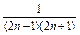 =
=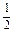
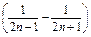 , ---------9分
, ---------9分
∴Tn=b1+b2+…+bn=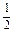
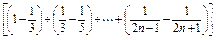 =
=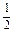
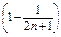 =
=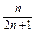 ---12分
---12分
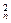 =an
=an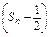 ,an=Sn-Sn-1(n≥2),
,an=Sn-Sn-1(n≥2),∴S
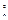 =(Sn-Sn-1)
=(Sn-Sn-1)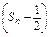 , 2Sn-1Sn=Sn-1-Sn, ① ---------2分
, 2Sn-1Sn=Sn-1-Sn, ① ---------2分 由题意Sn-1·S
 n≠0,①式两边同除以Sn-1·Sn ,得
n≠0,①式两边同除以Sn-1·Sn ,得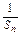 -
-
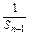 =2,------4分
=2,------4分∴数列
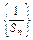 是首项为
是首项为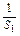 =
=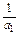 =1,公差为2的等差数列.
=1,公差为2的等差数列. ∴
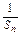 =1+2(n-1)=2n-1, --------5分
=1+2(n-1)=2n-1, --------5分∴Sn=
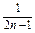 . ------6分
. ------6分(2)又bn=
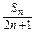 =
=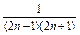 =
=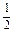
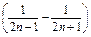 , ---------9分
, ---------9分 ∴Tn=b1+b2+…+bn=
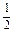
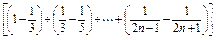 =
=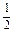
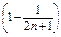 =
=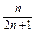 ---12分
---12分
练习册系列答案
相关题目
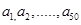 是从
是从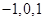 这三个整数中取值的数列. 若
这三个整数中取值的数列. 若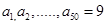 且
且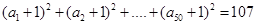 , 则
, 则 N*),满足条件:
N*),满足条件: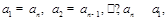 即
即 ,我们称其为“对称数列”.例如:数列1,2,3,4,3,2,1就是“对称数列”.已知数列
,我们称其为“对称数列”.例如:数列1,2,3,4,3,2,1就是“对称数列”.已知数列 是项数为不超过
是项数为不超过 的“对称数列”,并使得1,2,22,…,
的“对称数列”,并使得1,2,22,…, 依次为该数列中前连续的
依次为该数列中前连续的 项,则数列
项,则数列 可以是:
可以是: ①
① ;②
;② ; ③
; ③ ;④
;④ .
.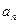 },{
},{ },{
},{ }满足a0=1,b0=1,c0=0,且
}满足a0=1,b0=1,c0=0,且 +2,
+2, ,
, +
+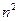 个数排成
个数排成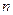 行
行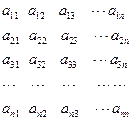
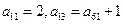 ,该数列第一列的
,该数列第一列的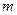 为公差的等差数列,每一行的
为公差的等差数列,每一行的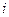 行第1列的数
行第1列的数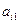 及第
及第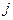 列的数
列的数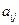
 为数列
为数列 的前n项和,且对任意
的前n项和,且对任意 都有
都有 ,记
,记
 ;
; 与
与 的大小;
的大小; 。
。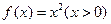 的图像上依次取点列
的图像上依次取点列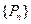 满足:
满足: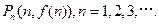 设
设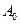 为平面上任意一点,若
为平面上任意一点,若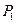 的对称点为
的对称点为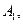
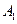 关于
关于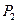 的对称点为
的对称点为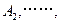 依次类推,可在平面上得相应点列
依次类推,可在平面上得相应点列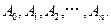 则当
则当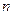 为偶数时,向量
为偶数时,向量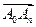 的坐标为_______________________.
的坐标为_______________________.