题目内容
 如图,从x轴与曲线y=-x2+2所围成的区或内任取一点M(x、y),则M取自阴影部分的概率为( )
如图,从x轴与曲线y=-x2+2所围成的区或内任取一点M(x、y),则M取自阴影部分的概率为( )分析:本题考查的知识点是几何概型的意义,关键是要找出阴影部分的面积,及x轴与曲线y=-x2+2所围成的区域的面积,再将它们代入几何概型计算公式计算出概率.
解答:解:联立曲线y=-x2+2与直线y=1的方程得到交点为(1,1),(-1,1)
故阴影部分面积S阴影=
(-x2+2-1)dx=2
(-x2+1)dx=2×
=
,
x轴与曲线y=-x2+2所围成的区域的面积S=
(-x2+2)dx=2
(-x2+2)dx=2×
=
,
∴M取自阴影部分的概率P=
=
=
,
故答案为:A
故阴影部分面积S阴影=
| ∫ | 1 -1 |
| ∫ | 1 0 |
| 2 |
| 3 |
| 4 |
| 3 |
x轴与曲线y=-x2+2所围成的区域的面积S=
| ∫ |
-
|
| ∫ |
0 |
4
| ||
| 3 |
8
| ||
| 3 |
∴M取自阴影部分的概率P=
| S阴影 |
| S |
| ||||
|
| ||
| 4 |
故答案为:A
点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=
求解.
| N(A) |
| N |

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
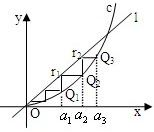 设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
 如图,从点P1(0,0)做x轴的垂线交曲线y=ex于点Q1(0,1),曲线在Q1点处的切线与x轴交于点P2,再从P2做x轴的垂线交曲线于点Q2,依次重复上述过程得到一系列点:P1,Q1;P2,Q2…;Pn,Qn,记Pk点的坐标为(xk,0)(k=1,2,…,n).
如图,从点P1(0,0)做x轴的垂线交曲线y=ex于点Q1(0,1),曲线在Q1点处的切线与x轴交于点P2,再从P2做x轴的垂线交曲线于点Q2,依次重复上述过程得到一系列点:P1,Q1;P2,Q2…;Pn,Qn,记Pk点的坐标为(xk,0)(k=1,2,…,n). 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.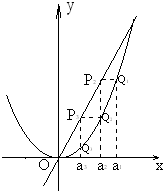 (2013•广州三模)如图,已知直线l:y=4x及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<4).从曲线C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
(2013•广州三模)如图,已知直线l:y=4x及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<4).从曲线C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.